Подробно о генераторах случайных и псевдослучайных чисел / Хабр

Введение

Генераторы случайных чисел — ключевая часть веб-безопасности. Небольшой список применений:

• Генераторы сессий(PHPSESSID)
• Генерация текста для капчи
• Шифрование
• Генерация соли для хранения паролей в необратимом виде
• Генератор паролей
• Порядок раздачи карт в интернет казино

Как отличить случайную последовательность чисел от неслучайной?

Пусть есть последовательность чисел: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 . Является ли она случайной? Есть строгое определение для случайной величины. Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать. Но оно не помогает ответить на наш вопрос, так как нам не хватает информации для ответа. Теперь скажем, что данные числа получились набором одной из верхних строк клавиатуры. «Конечно не случайная» — воскликните Вы и тут же назовете следующие число и будете абсолютно правы. Последовательность будет случайной только если между символами, нету зависимости. Например, если бы данные символы появились в результате вытягивания бочонков в лото, то последовательность была бы случайной.

Чуть более сложный пример или число Пи

Последовательность цифры в числе Пи считается случайной. Пусть генератор основывается на выводе бит представления числа Пи, начиная с какой-то неизвестной точки. Такой генератор, возможно и пройдет «тест на следующий бит», так как ПИ, видимо, является случайной последовательностью. Однако этот подход не является критографически надежным — если криптоаналитик определит, какой бит числа Пи используется в данный момент, он сможет вычислить и все предшествующие и последующие биты.
Данный пример накладывает ещё одно ограничение на генераторы случайных чисел. Криптоаналитик не должен иметь возможности предсказать работу генератора случайных чисел.

Отличие генератора псевдослучайных чисел (ГПСЧ) от генератора случайных чисел (ГСЧ)

Источники энтропии используются для накопления энтропии с последующим получением из неё начального значения (initial value, seed), необходимого генераторам случайных чисел (ГСЧ) для формирования случайных чисел. ГПСЧ использует единственное начальное значение, откуда и следует его псевдослучайность, а ГСЧ всегда формирует случайное число, имея в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
Энтропия – это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.
Можно сказать, что ГСЧ = ГПСЧ + источник энтропии.

Уязвимости ГПСЧ

• Предсказуемая зависимость между числами.
• Предсказуемое начальное значение генератора.
• Малая длина периода генерируемой последовательности случайных чисел, после которой генератор зацикливается.

Линейный конгруэнтный ГПСЧ(LCPRNG)

Распространённый метод для генерации псевдослучайных чисел, не обладающий криптографической стойкостью. Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:

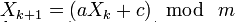
где a(multiplier), c(addend), m(mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа (seed) X0 и при разных его значениях получаются различные последовательности случайных чисел.

Для выбора коэффициентов имеются свойства позволяющие максимизировать длину периода(максимальная длина равна m), то есть момент, с которого генератор зациклится [1].

Пусть генератор выдал несколько случайных чисел X0, X1, X2, X3. Получается система уравнений

Решив эту систему, можно определить коэффициенты a, c, m. Как утверждает википедия [8], эта система имеет решение, но решить самостоятельно или найти решение не получилось. Буду очень признателен за любую помощь в этом направлении.

Предсказание результатов линейно-конгруэнтного метода

Основным алгоритмом предсказания чисел для линейно-конгруэнтного метода является Plumstead’s — алгоритм, реализацию, которого можно найти здесь [4](есть онлайн запуск) и здесь [5]. Описание алгоритма можно найти в [9].
Простая реализация конгруэнтного метода на Java.

Отправив 20 чисел на сайт [4], можно с большой вероятностью получить следующие. Чем больше чисел, тем больше вероятность.

Взлом встроенного генератора случайных чисел в Java

Многие языки программирования, например C(rand), C++(rand) и Java используют LСPRNG. Рассмотрим, как можно провести взлом на примере java.utils.Random. Зайдя в исходный код(jdk1.7) данного класса можно увидеть используемые константы

Метод java.utils.Randon.nextInt() выглядит следующим образом (здесь bits == 32)

Результатом является nextseed сдвинутый вправо на 48-32=16 бит. Данный метод называется truncated-bits, особенно неприятен при black-box, приходится добавлять ещё один цикл в brute-force. Взлом будет происходить методом грубой силы(brute-force).

Пусть мы знаем два подряд сгенерированных числа x1 и x2. Тогда необходимо перебрать 2^16 = 65536 вариантов oldseed и применять к x1 формулу:

до тех пор, пока она не станет равной x2. Код для brute-force может выглядеть так

Вывод данной программы будет примерно таким:

Несложно понять, что мы нашли не самый первый seed, а seed, используемый при генерации второго числа. Для нахождения первоначального seed необходимо провести несколько операций, которые Java использовала для преобразования seed, в обратном порядке.

И теперь в исходном коде заменим
crackingSeed.set(seed);
на
crackingSeed.set(getPreviousSeed(seed));

И всё, мы успешно взломали ГПСЧ в Java.

Взлом ГПСЧ Mersenne twister в PHP

Рассмотрим ещё один не криптостойкий алгоритм генерации псевдослучайных чисел Mersenne Twister. Основные преимущества алгоритма — это скорость генерации и огромный период 2^19937 − 1, На этот раз будем анализировать реализацию алгоритма mt_srand() и mt_rand() в исходном коде php версии 5.4.6.

Можно заметить, что php_mt_reload вызывается при инициализации и после вызова php_mt_rand 624 раза. Начнем взлом с конца, обратим трансформации в конце функции php_mt_rand(). Рассмотрим (s1 ^ (s1 >> 18)). В бинарном представление операция выглядит так:

10110111010111100111111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
10110111010111100101001110100101 s1 ^ (s1 >> 18)
Видно, что первые 18 бит (выделены жирным) остались без изменений.
Напишем две функции для инвертирования битового сдвига и xor

Тогда код для инвертирования последних строк функции php_mt_rand() будет выглядеть так

Если у нас есть 624 последовательных числа сгенерированных Mersenne Twister, то применив этот алгоритм для этих последовательных чисел, мы получим полное состояние Mersenne Twister, и сможем легко определить каждое последующее значение, запустив php_mt_reload для известного набора значений.

Область для взлома

Если вы думаете, что уже нечего ломать, то Вы глубоко заблуждаетесь. Одним из интересных направлений является генератор случайных чисел Adobe Flash(Action Script 3.0). Его особенностью является закрытость исходного кода и отсутствие задания seed’а. Основной интерес к нему, это использование во многих онлайн-казино и онлайн-покере.
Есть много последовательностей чисел, начиная от курса доллара и заканчивая количеством времени проведенным в пробке каждый день. И найти закономерность в таких данных очень не простая задача.

Задание распределения для генератора псевдослучайных чисел

Для любой случайной величины можно задать распределение. Перенося на пример с картами, можно сделать так, чтобы тузы выпадали чаще, чем девятки. Далее представлены несколько примеров для треугольного распределения и экспоненциального распределения.

Треугольное распределение

Приведем пример генерации случайной величины с треугольным распределением [7] на языке C99.

В данном случае мы берем случайную величину rand() и задаем ей распределение, исходя из функции треугольного распределения. Для параметров a = -40, b = 100, c = 50 график 10000000 измерений будет выглядеть так

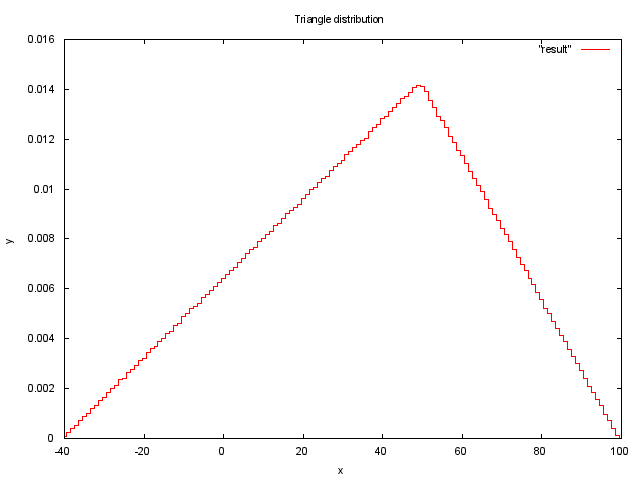
Экспоненциальное распределение

Пусть требуется получить датчик экспоненциально распределенных случайных величин. В этом случае F(x) = 1 – exp(-lambda * x). Тогда из решения уравнения y = 1 – exp(-lambda * x) получаем x = -log(1-y)/lambda.
Можно заметить, что выражение под знаком логарифма в последней формуле имеет равномерное распределение на отрезке [0,1), что позволяет получать другую, но так же распределённую последовательность по формуле: x = -log(y)/lambda, где y есть случайная величина(rand()).

Тесты ГПСЧ

Некоторые разработчики считают, что если они скроют используемый ими метод генерации или придумают свой, то этого достаточно для защиты. Это очень распространённое заблуждение. Следует помнить, что есть специальные методы и приемы для поиска зависимостей в последовательности чисел.

Одним из известных тестов является тест на следующий бит — тест, служащий для проверки генераторов псевдослучайных чисел на криптостойкость. Тест гласит, что не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью большей ½.

В теории криптографии отдельной проблемой является определение того, насколько последовательность чисел или бит, сгенерированных генератором, является случайной. Как правило, для этой цели используются различные статистические тесты, такие как DIEHARD или NIST. Эндрю Яо в 1982 году доказал, что генератор, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность, выполнимые за полиномиальное время.
В интернете [10] можно пройти тесты DIEHARD и множество других, чтобы определить критостойкость алгоритма.

Что такое псевдослучайные числа

Никакой детерминированный алгоритм не может генерировать полностью случайные числа, он может только аппроксимировать некоторые свойства случайных чисел. Как сказал Джон фон Нейман, «всякий, кто питает слабость к арифметическим методам получения случайных чисел, грешен вне всяких сомнений».

Любой ГПСЧ с ограниченными ресурсами рано или поздно зацикливается — начинает повторять одну и ту же последовательность чисел. Длина циклов ГПСЧ зависит от самого генератора и в среднем составляет около 2 n/2 , где n — размер внутреннего состояния в битах, хотя линейные конгруэнтные и LFSR-генераторы обладают максимальными циклами порядка 2 n . Если ГПСЧ может сходиться к слишком коротким циклам, такой ГПСЧ становится предсказуемым и является непригодным.

Большинство простых арифметических генераторов хотя и обладают большой скоростью, но страдают от многих серьёзных недостатков:

• Слишком короткий период/периоды.
• Последовательные значения не являются независимыми.
• Некоторые биты «менее случайны», чем другие.
• Неравномерное одномерное распределение.
• Обратимость.

В частности, алгоритм мейнфреймах, оказался очень плохим [1] [2] , что вызвало сомнения в достоверности результатов многих исследований, использовавших этот алгоритм.

Из современных ГПСЧ широкое распространение получил «вихрь Мерсенна», предложенный в 1997 году Мацумото и Нишимурой. Его достоинствами являются колоссальный период (2 19937 -1), равномерное распределение в 623 измерениях (линейный конгруэнтный метод даёт более или менее равномерное распределение от силы в 5 измерениях), быстрая генерация случайных чисел (в 2-3 раза быстрее, чем стандартные ГПСЧ, использующие линейный конгруэнтный метод). Однако существуют сложные алгоритмы, распознающие последовательность, порождаемую с помощью вихря Мерсенна, как неслучайную. Это делает вихрь Мерсенна неподходящим для криптографии.

ГПСЧ с источником энтропии или ГСЧ

Наравне с существующей необходимостью генерировать легко воспроизводимые последовательности случайных чисел, также существует необходимость генерировать совершенно непредсказуемые или попросту абсолютно случайные числа. Такие генераторы называются генераторами случайных чисел (ГСЧ — англ. random number generator, RNG ). Так как такие генераторы чаще всего применяются для генерации уникальных симметричных и асимметричных ключей для шифрования, они чаще всего строятся из комбинации криптостойкого ГПСЧ и внешнего источника энтропии (и именно такую комбинацию теперь и принято понимать под ГСЧ).

Почти все крупные производители микрочипов поставляют аппаратные ГСЧ с различными источниками энтропии, используя различные методы для их очистки от неизбежной предсказуемости. Однако на данный момент скорость сбора случайных чисел всеми существующими микрочипами (несколько тысяч бит в секунду) не соответствует быстродействию современных процессоров.

В персональных компьютерах авторы программных ГСЧ используют гораздо более быстрые источники энтропии, такие, как шум звуковой карты или счётчик тактов процессора. До появления возможности считывать значения счётчика тактов, сбор энтропии являлся наиболее уязвимым местом ГСЧ. Эта проблема до сих пор полностью не разрешена во многих устройствах (например, смарт-картах), которые таким образом остаются уязвимыми. Многие ГСЧ до сих пор используют традиционные (устаревшие) методы сбора энтропии вроде измерения реакции пользователя (движение мыши и т. п.), как, например, в [3] , или взаимодействия между потоками, как, например, в Java secure random.

Примеры ГСЧ и источников энтропии

Несколько примеров ГСЧ с их источниками энтропии и генераторами:

Источник энтропии	ГПСЧ	Достоинства	Недостатки
/dev/random в Linux	Счётчик тактов процессора, однако собирается только во время аппаратных прерываний	LFSR, с хешированием выхода через	Очень долго «нагревается», может надолго «застревать», либо работает как ГПСЧ (/dev/urandom)
Yarrow от Брюса Шнайера [3]	Традиционные (устаревшие) методы	AES-256 и	Гибкий криптостойкий дизайн	Долго «нагревается», очень маленькое внутреннее состояние, слишком сильно зависит от криптостойкости выбранных алгоритмов, медленный, применим исключительно для генерации ключей
Генератор Леонида Юрьева [4]	Шум звуковой карты	?	Скорее всего, хороший и быстрый источник энтропии	Нет независимого, заведомо криптостойкого ГПСЧ, доступен исключительно в виде Windows
Microsoft		Встроен в Windows, не «застревает»	Маленькое внутреннее состояние, легко предсказуем
	Взаимодействие между потоками		В Java другого выбора пока нет, большое внутреннее состояние	Медленный сбор энтропии
Chaos от Ruptor [5]	Счётчик тактов процессора, собирается непрерывно	Хеширование 4096-битового внутреннего состояния на основе нелинейного варианта Marsaglia-генератора	Пока самый быстрый из всех, большое внутреннее состояние, не «застревает»
RRAND от Ruptor [6]	Счётчик тактов процессора	Зашифровывание внутреннего состояния поточным шифром	Очень быстр, внутреннее состояние произвольного размера по выбору, не «застревает»

ГПСЧ в криптографии

Разновидностью ГПСЧ являются ГПСБ (PRBG) — генераторы псевдо-случайных бит, а так же различных поточных шифров. ГПСЧ, как и поточные шифры, состоят из внутреннего состояния (обычно размером от 16 бит до нескольких мегабайт), функции инициализации внутреннего состояния ключом или семенем (англ. seed ), функции обновления внутреннего состояния и функции вывода. ГПСЧ подразделяются на простые арифметические, сломанные криптографические и криптостойкие. Их общее предназначение — генерация последовательностей чисел, которые невозможно отличить от случайных вычислительными методами.

Хотя многие криптостойкие ГПСЧ или поточные шифры предлагают гораздо более «случайные» числа, такие генераторы гораздо медленнее обычных арифметических и могут быть непригодны во всякого рода исследованиях, требующих, чтобы процессор был свободен для более полезных вычислений.

В военных целях и в полевых условиях применяются только засекреченные синхронные криптостойкие ГПСЧ (поточные шифры), блочные шифры не используются. Примерами известных криптостойких ГПСЧ являются ISAAC, SEAL, Snow, совсем медленный теоретический алгоритм Блюма, Блюма и Шуба, а так же счётчики с криптографическими хеш-функциями или криптостойкими блочными шифрами вместо функции вывода.

Аппаратные ГПСЧ

Кроме устаревших, хорошо известных LFSR-генераторов, широко применявшихся в качестве аппаратных ГПСЧ в XX веке, к сожалению, очень мало известно о современных аппаратных ГПСЧ (поточных шифрах), так как большинство из них разработано для военных целей и держатся в секрете. Почти все существующие коммерческие аппаратные ГПСЧ запатентованы и также держатся в секрете. Аппаратные ГПСЧ ограничены строгими требованиями к расходуемой памяти (чаще всего использование памяти запрещено), быстродействию (1-2 такта) и площади (несколько сотен FPGA- или

Из-за недостатка хороших аппаратных ГПСЧ производители вынуждены применять имеющиеся под рукой гораздо более медленные, но широко известные блочные шифры (

Примечания

1. ↑Дональд Кнут. Глава 3.3. Спектральный критерий // Искусство программирования. Указ. соч. — С. 129—130.
2. ↑William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery. Numerical Recipes in C: The Art of Scientific Computing. — 2nd ed. — Cambridge University Press, 1992. — P. 277. — ISBN 0-521-43108-5
3. ↑ 12http://www.schneier.com/yarrow.html
4. ↑http://leo.yuriev.ru/random
5. ↑http://cryptolib.com/crypto/chaos/
6. ↑http://cryptolib.com/crypto/rrand/

См. также

• NIST STS — пакет статистического тестирования
• CryptX — пакет статистического тестирования
• Тесты DIEHARD
• Метод Монте-Карло
• Случайное простое число
• Линейный конгруэнтный метод

Ссылки

• Андрей Зубинский. В поисках случайности Компьютерное обозрение № 29 (2003)
• Юрий Лифшиц. Курс «Современные задачи криптографии» Лекция 9: Псевдослучайные генераторы
• Л. Бараш. Алгоритм AKS проверки чисел на простоту и поиск констант генераторов псевдослучайных чисел
• noonv. Старый взгляд на новые вещи
• Жельников Владимир. Псевдослучайные последовательности чисел // Криптография от папируса до компьютера М.: ABF, 1996.
• random.org (англ.) — онлайновый сервис для генерации случайных чисел
• Cryptographic Random Numbers (англ.)
• Theory and Practice of Random Number Generation (англ.)
• Zvi Gutterman, Benny Pinkas, Tzachy Reinman. Analysis of the Linux Random Number Generator (англ.)
• A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications (англ.) NIST SP 800-22

Литература

• Дональд Кнут. Глава 3. Случайные числа // Искусство программирования = The Art of Computer Programming. — 3-е изд. — М.: «Вильямс», 2007. — Т. 2. Получисленные алгоритмы. — 832 с. — ISBN 5-8459-0081-6 (русс.) ISBN 0-201-89684-2 (англ.)

Wikimedia Foundation . 2010 .

• Псевдосоляризация
• Псевдотуберкулез

Смотреть что такое «Псевдослучайные числа» в других словарях:

псевдослучайные числа — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] псевдослучайные числа псевдослучайные величины Вырабатываемая алгоритмически последовательность чисел, обладающих свойствами случайных чисел и используемых взамен последних при … Справочник технического переводчика

Псевдослучайные числа — [pse­udo random numbers], псевдослучайные величины вырабатываемая алгоритмически последовательность чисел, обладающих свойствами случайных чисел и используемых взамен последних при решении на ЭВМ ряда классов задач (см., например, Метод Мон­те… … Экономико-математический словарь

ПСЕВДОСЛУЧАЙНЫЕ ЧИСЛА — см. Случайные и псевдослучайные числа … Математическая энциклопедия

СЛУЧАЙНЫЕ И ПСЕВДОСЛУЧАЙНЫЕ ЧИСЛА — числа (или цифры ), последовательность появления к рых обладает теми или иными статистич. закономерностями (см. Вероятностей теория). Различают случайные числа (с. ч.), генерируемые каким либо стохастич. устройством, и псевдослучайные числа (п. ч … Математическая энциклопедия

Случайные и псевдослучайные числа — числа, которые могут рассматриваться в качестве реализации некоторой случайной величины (См. Случайная величина). Как правило, имеются в виду реализации случайной величины, равномерно распределенной на промежутке (0,1), или приближения к… … Большая советская энциклопедия

Алгоритмы уничтожения информации — Алгоритмы уничтожения информации последовательность операций, предназначенных для осуществления программными и/или аппаратными средствами необратимого удаления данных, в том числе остаточной информации. Как правило, данные алгоритмы… … Википедия

Генератор псевдослучайных чисел — (ГПСЧ, англ. Pseudorandom number generator, PRNG) алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному). Современная информатика… … Википедия

Датчик случайных чисел — Генератор псевдослучайных чисел (ГПСЧ, англ. Pseudorandom number generator, PRNG) алгоритм, генерирующий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).… … Википедия

Криптостойкий генератор псевдослучайных чисел — Генератор псевдослучайных чисел (ГПСЧ, англ. Pseudorandom number generator, PRNG) алгоритм, генерирующий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).… … Википедия

Псевдослучайное число — Генератор псевдослучайных чисел (ГПСЧ, англ. Pseudorandom number generator, PRNG) алгоритм, генерирующий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).… … Википедия

Как компьютер генерирует случайные числа

Что такое случайность в компьютере? Как происходит генерация случайных чисел? В этой статье мы постарались дать простые ответы на эти вопросы.

В программном обеспечении, да и в технике в целом существует необходимость в воспроизводимой случайности: числа и картинки, которые кажутся случайными, на самом деле сгенерированы определённым алгоритмом. Это называется псевдослучайностью, и мы рассмотрим простые способы создания псевдослучайных чисел. В конце статьи мы сформулируем простую теорему для создания этих, казалось бы, случайных чисел.

Определение того, что именно является случайностью, может быть довольно сложной задачей. Существуют тесты (например, колмогоровская сложность), которые могут дать вам точное значение того, насколько случайна та или иная последовательность. Но мы не будем заморачиваться, а просто попробуем создать последовательность чисел, которые будут казаться несвязанными между собой.

Часто требуется не просто одно число, а несколько случайных чисел, генерируюемых непрерывно. Следовательно, учитывая начальное значение, нам нужно создать другие случайные числа. Это начальное значение называется семенем, и позже мы увидим, как его получить. А пока давайте сконцентрируемся на создании других случайных значений.

Создание случайных чисел из семени

Один из подходов может заключаться в том, чтобы применить какую-то безумную математическую формулу к семени, а затем исказить её настолько, что число на выходе будет казаться непредсказуемым, а после взять его как семя для следующей итерации. Вопрос только в том, как должна выглядеть эта функция искажения.

Давайте поэкспериментируем с этой идеей и посмотрим, куда она нас приведёт.

Функция искажения будет принимать одно значение, а возвращать другое. Назовём её R.

Начнём с того, что R — это простая функция, которая всего лишь прибавляет единицу.

Если значение нашего семени 1, то R создаст ряд 1, 2, 3, 4, . Выглядит совсем не случайно, но мы дойдём до этого. Пусть теперь R добавляет константу вместо 1.

Если с равняется, например, 7, то мы получим ряд 1, 8, 15, 22, . Всё ещё не то. Очевидно, что мы упускаем то, что числа не должны только увеличиваться, они должны быть разбросаны по какому-то диапазону. Нам нужно, чтобы наша последовательность возвращалась в начало — круг из чисел!

Числовой круг

Посмотрим на циферблат часов: наш ряд начинается с 1 и идёт по кругу до 12. Но поскольку мы работаем с компьютером, пусть вместо 12 будет 0.

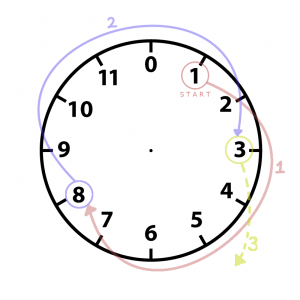
Теперь начиная с 1 снова будем прибавлять 7. Прогресс! Мы видим, что после 12 наш ряд начинает повторяться, независимо от того, с какого числа начать.

Здесь мы получаем очень важно свойство: если наш цикл состоит из n элементов, то максимальное число элементов, которые мы можем получить перед тем, как они начнут повторяться это n.

Теперь давайте переделаем функцию R так, чтобы она соответствовала нашей логике. Ограничить длину цикла можно с помощью оператора модуля или оператора остатка от деления.

На этом этапе вы можете заметить, что некоторые числа не подходят для c. Если c = 4, и мы начали с 1, наша последовательность была бы 1, 5, 9, 1, 5, 9, 1, 5, 9, . что нам конечно же не подходит, потому что эта последовательность абсолютно не случайная. Становится понятно, что числа, которые мы выбираем для длины цикла и длины прыжка должны быть связаны особым образом.

Если вы попробуете несколько разных значений, то сможете увидеть одно свойство: m и с должны быть взаимно простыми.

До сих пор мы делали «прыжки» за счёт добавления, но что если использовать умножение? Умножим х на константу a.

Свойства, которым должно подчиняться а, чтобы образовался полный цикл, немного более специфичны. Чтобы создать верный цикл:

1. (а — 1) должно делиться на все простые множители m
2. (а — 1) должно делиться на 4, если m делится на 4

Эти свойства вместе с правилом, что m и с должны быть взаимно простыми составляют теорему Халла-Добелла. Мы не будем рассматривать её доказательство, но если бы вы взяли кучу разных значений для разных констант, то могли бы прийти к тому же выводу.

Выбор семени

Настало время поговорить о самом интересном: выборе первоначального семени. Мы могли бы сделать его константой. Это может пригодиться в тех случаях, когда вам нужны случайные числа, но при этом нужно, чтобы при каждом запуске программы они были одинаковые. Например, создание одинаковой карты для каждой игры.

Еще один способ — это получать семя из нового источника каждый раз при запуске программы, как в системных часах. Это пригодится в случае, когда нужно общее рандомное число, как в программе с бросанием кубика.

Конечный результат

Когда мы применяем функцию к её результату несколько раз, мы получаем рекуррентное соотношение. Давайте запишем нашу формулу с использованием рекурсии:

Где начальное значение х — это семя, а — множитель, с — константа, m — оператор остатка от деления.

То, что мы сделали, называется линейным конгруэнтным методом. Он очень часто используется, потому что он прост в реализации и вычисления выполняются быстро.

В разных языках программирования реализация линейного конгруэнтного метода отличается, то есть меняются значения констант. Например, функция случайных чисел в libc (стандартная библиотека С для Linux) использует m = 2 ^ 32, a = 1664525 и c = 1013904223. Такие компиляторы, как gcc, обычно используют эти значения.

Заключительные замечания

Существуют и другие алгоритмы генерации случайных чисел, но линейный конгруэнтный метод считается классическим и лёгким для понимания. Если вы хотите глубже изучить данную тему, то обратите внимание на книгу Random Numbers Generators, в которой приведены элегантные доказательства линейного конгруэнтного метода.

Генерация случайных чисел имеет множество приложений в области информатики и особенно важна для криптографии.

Псевдослучайные числа

Функции rand() и srand()

В языках программирования обычно предусмотрены функции, позволяющие генерировать случайные числа в определенном по умолчанию диапазоне. На самом деле генерируются не случайные, а так называемые псевдослучайные числа; они выглядят случайно, но вычисляются по вполне конкретной формуле. Но для простоты далее мы все равно будем называть их случайными.

В языке программирования C получить случайное число можно с помощью функции rand() , которая входит в стандартную библиотеку языка. Эта функция не принимает никакие параметры.

Задание
Напишите программу, в которой целочисленной переменной присваивается результат выполнения функции rand() . Выведите значение переменной на экран.

Функция rand() возвращает целое число от 0 до значения присвоенного константе RAND_MAX. Значение RAND_MAX зависит от системы и определено в заголовочном файле stdlib.h. Так, например, оно может быть равно 32767 (двухбайтовое целое) или 2147483647 (четырехбайтовое целое).

Задание
Определите значение RAND_MAX в вашей системе. Для этого не забудьте подключить к файлу исходного кода заголовочный файл stdlib.h.

Код ниже выводит на экран 50 случайных чисел:

В теле цикла осуществляется переход на новую строку после каждых выведенных на экран пяти чисел. Для этого используется выражение, в котором находится остаток от деления i на 5, результат сравнивается с 0. Чтобы после первого числа не происходил переход на новую строку, iсначала присваивается единица, а не ноль (т.к. 0 делится на 5 без остатка).

Задание
Спишите код, приведенный выше. Выполните программу несколько раз, при этом обратите внимание, разные ли результаты вы получаете от выполнения к выполнению.

Вы должны были заметить, что при каждом запуске программы числа остаются одинаковыми. Даже если вы перекомпилируете программу, результат не изменится. Данный эффект связан с тем, что начальное (инициализирующее) число, которое подставляется в формулу вычисления первого и последующих псевдослучайных чисел, для каждой системы всегда одно и то же. Однако это начальное число можно изменить с помощью функции srand() , которой в качестве параметра передается любое целое число. Понятно, что если вы зададите конкретный аргумент для функции, например, srand(1000) , то от вызова к вызову программы числа будут также одни и те же. Хотя и не те, что были бы без srand() . Поэтому появляется проблема, как сделать так, чтобы аргумент для srand() был тоже случайным? Получается замкнутый круг.

Задание
Переделайте программу, выводящую на экран 50 случайных чисел так, чтобы сначала у пользователя запрашивалось любое целое число с помощью scanf() , которое передавалось бы в функцию srand() .

Пользователь программы сам может задавать инициализирующее значение. Но чаще всего это не является полноценным выходом из ситуации. Поэтому инициализирующее значение привязывают к какому-либо процессу, протекающему в операционной системе, например, к часам. Время (учитывая не только время суток, но и дату) никогда не бывает одинаковым. Значит значение для srand() , преобразованное в целое из системного времени, будет различным.

Текущее время можно узнать с помощью функции time() , прототип которой описан в файле time.h. Передав time() в качестве параметра NULL, мы получим целое число, которое можно передать в srand() :
srand(time(NULL));

Задание
Переделайте вашу программу так, чтобы инициализирующее значение зависело от системного времени.

Получение целых случайных чисел в заданных диапазонах

Функция rand() выдает случайное число от 0 до значения RAND_MAX. Что делать, если требуется получать случайные числа в иных диапазонах, например, от 100 до 999?

Сначала рассмотрим более простую ситуацию: получить случайные числа от 0 до 5. Если любое целое число попытаться разделить на 5 нацело, то можно получить как 0 (когда число делится на 5 без остатка), так и 1, 2, 3, 4. Например, rand() вернула число 283. Применяя к этому числу операцию нахождения остатка от деления на 5, получим 3. Т.е. выражение rand() % 5 дает любое число в диапазоне [0, 5).

Однако, что если надо, чтобы число 5 так же входило в диапазон, т.е. диапазон имеет вид [0, 5]? Логично предположить, что следует найти остаток от деления на 6. При этом более грамотным будет следующее рассуждение: надо находить остаток от деления на размер диапазона. В данном случае он равен шести значениям: 0, 1, 2, 3, 4, 5. Чтобы найти размер диапазона надо из допустимого максимума вычесть допустимый минимум и прибавить единицу: max — min + 1. Будьте внимательны: если, например, требуется, чтобы указанный в задаче максимум не входил в диапазон, то единицу прибавлять не надо или надо вычитать единицу из максимума.

Задание
Напишите программу, выдающую 50 случайных чисел от 0 до 99 включительно.

Итак, мы знаем формулу получения длины диапазона: max — min + 1. Если требуется получить число от 6 до 10 включительно, то длина диапазона будет равна 10 — 6 + 1 = 5. Выражение rand()% 5 даст любое число от 0 до 4 включительно. Но нам надо от 6 до 10. В таком случае достаточно к полученному случайному остатку прибавить 6, т.е. минимум. Другими словами, надо выполнить сдвиг. Действительно для приведенного примера:

• если остаток был равен 0, то добавляя 6, получаем 6;
• остаток 1, добавляем 6, получаем 7;
• …
• остаток 4, прибавляем 6, получаем 10;
• остатка больше 4 не может быть.

В таком случае формула для получения случайного числа в диапазоне [a, b] выглядит так:

где длина_диапазона вычисляется как b — a + 1, сдвиг является значением a.

В эту формулу также вписываются случаи, когда необходимо получить случайное число от 0 до N, т.е. они являются ее частными случаями.

Задание
Выведите на экран ряд случайных чисел, принадлежащих диапазону от 100 до 299 включительно.

С таким же успехом можно получать случайные отрицательные числа. Действительно, если диапазон задан как [-35, -1], то его длина будет равна -1 — (-35) + 1 = 35, что соответствует действительности; выражение получения случайного числа будет выглядеть так:

Так, если остаток от деления составил 0, то мы получим -35, а если 34, то -1. Остальные остатки дадут значения в промежутке от -35 до -1.

Задание
Выведите на экран ряд случайных чисел, принадлежащих диапазону от -128 до 127 включительно.

Получение вещественных случайных чисел

Ситуация с вещественными числами выглядит несколько по-иному. Во-первых, мы не можем получить остаток от деления, если делимое или делитель дробное число. Во вторых при вычислении длины диапазона нельзя прибавлять единицу.

Поясним вторую причину. Допустим диапазон задан как [2.50, 5.30]. Он состоит не из определенного количества чисел (как в случае целых), а из неопределенного (можно сказать, бесконечного) числа значений, т.к. вещественные числа можно представлять с различной степенью точности. Позже выполняя округление все равно будет шанс получить максимальную границу диапазона, поэтому для вычисления длины диапазона достаточно из максимума вычесть минимум.

Если разделить случайное число, преобразованное к вещественному типу, которое выдала функция rand() , на значение константы RAND_MAX, то получится вещественное случайное число от 0 до 1. Теперь, если это число умножить на длину диапазона, то получится число, лежащее в диапазоне от 0 до значения длины диапазона. Далее если прибавить к нему смещение к минимальной границе, то число благополучно впишется в требуемый диапазон. Таким образом формула для получения случайного вещественного числа выглядит так:

(float) rand() / RAND_MAX * (max — min) + min

Задание
Заполните массив случайными числами в диапазоне от 0.51 до 1.00. Выведите значение элементов массива на экран.

Равновероятные случайные числа

Функция rand() генерирует любое случайное число от 0 до RAND_MAX с равной долей вероятности. Другими словами, у числа 100 есть такой же шанс выпасть, как и у числа 25876.

Чтобы доказать это, достаточно написать программу, подсчитывающую количество выпадений каждого из значений. Если выборка (количество «испытуемых») будет достаточно большой, а диапазон (разброс значений) маленьким, то мы должны увидеть, что процент выпадений того или иного значения приблизительно такой же как у других.

В приведенной программе массив из пяти элементов сначала заполняется нулями. Случайные числа генерируются от 0 до 4 включительно. Если выпадает число 0, то увеличивается значение первого элемента массива, если число 1, то второго, и т.д. В конце на экран выводится процент выпадения каждого из чисел.

Задание
Спишите данную программу. Посмотрите на результат ее выполнения при различных значениях N: 10, 50, 500, 5000, 50000. Объясните увиденное.

Генераторы случайных и псевдослучайных чисел

Рубрика: 1. Информатика и кибернетика

Опубликовано в

Дата публикации: 05.11.2017

Статья просмотрена: 1444 раза

Библиографическое описание:

Дроздова, И. И. Генераторы случайных и псевдослучайных чисел / И. И. Дроздова, В. В. Жилин. — Текст : непосредственный // Технические науки в России и за рубежом : материалы VII Междунар. науч. конф. (г. Москва, ноябрь 2017 г.). — Москва : Буки-Веди, 2017. — С. 13-16. — URL: https://moluch.ru/conf/tech/archive/286/13233/ (дата обращения: 17.06.2020).

Те, кто знаком с криптографией, прекрасно понимают важность случайных чисел. Практически каждый алгоритм шифрования содержит как минимум один параметр с характеристиками «случайное число». Алгоритмы формирования электронно-цифровых подписей используют случайные числа для формирования ключей. При чём требования к этим числам крайне строгие, ведь от их выполнения зависит криптостойкость всей системы шифрования. Обычный пользователь не может себе представить важность случайного числа в его жизни. Однако, каждый из нас ежедневно отправляет сообщения в интернете, совершает телефонные звонки, но никто не хочет, чтобы третья сторона знала о чём ведётся беседа. Шифрование данных применяется не только для сокрытия важной государственной информации, данные каждого человека ежедневно подвергаются шифрованию. Поэтому нельзя недооценивать роль случайного числа в жизни современного человека. Это обстоятельство подчёркивает известный афоризм математика ORNL Роберта Кавью: «генерация случайных чисел слишком важна, чтобы оставлять её на волю случая».

Что же такое генератор псевдослучайных чисел — это алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).

Известно, что при реализации криптографических преобразований, используют различные случайные первичные состояния либо целые последовательности. Отсюда следует, что стойкость криптопреобразования напрямую зависит от алгоритма формирования случайных чисел и последовательностей, точнее от их степени случайности.

Современные компиляторы обладают собственной реализацией генератора псевдослучайных последовательностей, однако с криптографической точки зрения они являются непригодными. Основная сложность генерации последовательности псевдослучайных чисел на компьютере в том, что компьютеры детерминистичны по своей сути. Компьютер может находиться только в конечном количестве состояний (количество состояний огромно, но все-таки конечно). Следовательно, любой датчик случайных чисел по определению периодичен. Все периодическое — предсказуемо, т. е. не случайно.

Лучшее, что может произвести компьютер — это псевдослучайная последовательность. Период такой последовательности должен быть таким, чтобы конечная последовательность разумной длины не была периодической. Относительно короткие непериодические подпоследовательности должны быть как можно более неотличимы от случайных последовательностей, в частности, соответствовать различным критериям случайности.

Источники настоящих случайных чисел найти крайне трудно. Физические шумы, такие, как детекторы событий ионизирующей радиации, дробовой шум в резисторе или космическое излучение, могут быть такими источниками. Однако применяются такие устройства в приложениях сетевой безопасности редко. Сложности также вызывают грубые атаки на подобные устройства.

Криптографические приложения используют для генерации случайных чисел особенные алгоритмы. Эти алгоритмы заранее определены и, следовательно, генерируют последовательность чисел, которая теоретически не может быть статистически случайной. В то же время, если выбрать хороший алгоритм, полученная численная последовательность — псевдослучайных чисел — будет проходить большинство тестов на случайность. Одной из характеристик такой последовательности является период повторения, который должен быть больше рабочего интервала, из которого берутся числа.

Альтернативным решением является создание набора из большого количества случайных чисел и опубликование его в некотором словаре, называемом «одноразовым блокнотом». Тем не менее, и такие наборы обеспечивают очень ограниченный источник чисел по сравнению с тем количеством, которое требуется приложениям сетевой безопасности. Хотя данные наборы действительно обеспечивают статистическую случайность, они недостаточно безопасны, так как злоумышленник может получить копию словаря.

В большинстве алгоритмов шифрования, особенно потоковых шифрах, используются генераторы ключевой последовательности. Генератор ключевой последовательности выдает поток битов, который выглядит случайными, но в действительности является детерминированным и может быть в точности воспроизведен на стороне получателя. Чем больше генерируемый поток похож на случайный, тем больше времени потребуется криптоаналитику для взлома шифра.

Однако, если каждый раз при включении генератор будет выдавать одну и ту же последовательность, то взлом криптосистемы будет тривиальной задачей. Например, в случае использования потокового шифрования, перехватив два шифрованных текста, злоумышленник может сложить их по модулю 2 и получить два исходных текста, сложенных также по модулю 2. Такую систему раскрыть очень просто. Если же в руках противника окажется пара «исходный текст — шифрованный текст», то задача вообще становится тривиальной.

Поэтому все генераторы случайных последовательностей имеют зависимость от ключа. В этом случае простой криптоанализ будет невозможным. Структуру генератора ключевой последовательности можно представить в виде конечного автомата с памятью, состоящего из трех блоков:

‒ блока памяти, хранящего информацию о состоянии генератора,

‒ выходной функции, генерирующей бит ключевой последовательности в зависимости от состояния,

‒ функции переходов, задающей новое состояние, в которое перейдет генератор на следующем шаге.

В настоящее время насчитывается несколько тысяч различных вариантов генераторов псевдослучайных чисел.

Однако, не все из них могут применяться для решения задач криптографии. Существует отдельный класс таких устройств — криптографически стойкие генераторы псевдослучайных чисел. Они применяются для множества задач, например:

‒ Одноразовые случайные числа,

‒ Соль в схемах цифровой подписи, например, ECDSA.

Требуемое «качество» случайности меняется от задачи к задаче. Например, генерация одного случайного числа в некоторых протоколах требует только уникальности, тогда как генерация мастер-ключа или одноразового шифроблокнота требует высокой энтропии. В идеале, генерация случайных чисел в КСГПСЧ использует высоконадёжный источник энтропии, которым может быть аппаратный генератор случайных чисел или ход непредсказуемых процессов в системе — хотя в обоих случаях возможны неожиданные уязвимости. С точки зрения теории информации количество случайности — энтропия, которая может быть получена, равна энтропии, предоставляемой системой. Но зачастую в реальных ситуация требуется больше случайных чисел, чем можно получить при существующей энтропии. К тому же процедура получения случайности из самой системы требует достаточно много ресурсов (памяти и времени). В таких случаях, оправданно использование КСГПСЧ — это позволяет «растянуть» имеющуюся энтропию на большее число бит. Когда вся энтропия доступна до выполнения криптографического алгоритма, получается потоковый шифр. Однако некоторые криптосистемы позволяют добавлять энтропию по мере работы, в таком случае алгоритм не является эквивалентом потокового шифра и не может использоваться в этом качестве. Таким образом, разработка потоковых шифров и КСГПСЧ тесно связаны.

Основная идея криптографически стойких генераторов псевдослучайных чисел в том, что они идеально подходят для потоковых шифров. Выход таких генераторов неотличим (точнее, должен быть неотличим) от настоящих случайных последовательностей. С другой стороны, они детерминистичны.

Известно 4 подхода к их конструированию:

Эти подходы различаются в своих предположениях о возможностях криптоанализа, определении криптографического успеха и понятия надежности. Большая часть исследований в этой области теоретическая, хотя среди многих непрактичных генераторов существуют и удачные варианты.

В системно-теоретическом подходе, криптограф создает генератор ключевого потока, у которого есть проверяемые свойства — период, распределение битов, линейная сложность и т. д. криптограф изучает также различные методы криптоанализа и оптимизирует генератор против этих атак. Этот подход выработал набор критериев для потоковых шифров:

‒ Большой период, отсутствие повторений;

‒ Критерий линейной сложности: повышенная линейная сложность, локальная линейная сложность (Линейная сложность генератора — это длина кратчайшего LFSR, которая может сгенерировать выход генератора; линейная сложность есть мера случайности псевдослучайного генератора);

‒ Статистические критерии, такие как идеальное распределение:

• Перемешивание: любой бит ключевого потока должен быть сложным;
• преобразованием всех или большинства битов ключа;
• Рассеивание: избыточность в подструктурах должна рассеиваться;
• Нелинейные критерии (расстояние до линейных функций, критерий лавинообразности и т. д.).

В общем, этот список критериев годится не только для потоковых шифров, созданных в рамках системно-теоретического подхода, но и для всех потоковых шифров. Более того, эти критерии годятся и для всех блочных шифров. Но при системно- теоретическом подходе потоковые шифры создаются таким образом, чтобы напрямую удовлетворять вышеописанным критериям.

Основная проблема подобных криптосистем в том, что для них трудно доказать какие-либо факты об их криптостойкости. Дело в том, что для всех этих критериев не была доказана их необходимость или достаточность. Потоковый шифр может удовлетворять всем этим принципам и все-таки оказаться нестойким.

С другой стороны, взлом каждой такой системы — отдельная задача. Если бы таких шифров было много, то криптоаналитикам могло бы и не захотеться их атаковать. В конце концов, потоковые шифры во многом похожи на блочные шифры — для них нет доказательств стойкости. Существует набор известных способов атаки, но стойкость к ним ничего не гарантирует.

Самый лучший способ получить случайное число — это обратиться к естественной случайности реального мира — радиоактивный распад, шумные диоды и т. п. В принципе, элемент случайности есть и в компьютерах:

‒ время прибытия сетевых пакетов и т. п.

Проблема не в том, чтобы найти источники случайности, но в том, чтобы сохранить случайность при измерениях. Поэтому можно сделать вывод о сложности решения данной задачи и на текущем этапе развития вычислительной техники создание истинно случайной последовательности является практически неразрешимой задачей. Однако, важность подобных генераторов невозможно переоценить и качество построения псевдослучайных последовательностей возрастает с каждым днём.

1. Долгов В. И. Криптографическая защита информации в АСУ СН. —:, 1998. — с.
2. Дональд Э. Кнут. Глава 3. Случайные числа // Искусство программирования. — 3-е изд. — М.: Вильямс, 2000. — 832 с.
3. Жельников В. Псевдослучайные последовательности чисел // Кpиптография от папируса до компьютера. — М.: ABF, 1996. — 335 с.

Похожие статьи

Методы генерации случайных чисел | Статья в журнале.

Компьютер справляется с задачей построения последовательности случайных чисел гораздо лучше. Все генераторы случайных чисел делятся на два вида: ‒ True random number generator (ГНСЧ, генератор настоящих случайных чисел).

Методология сравнения потоковых шифров | Статья в журнале.

Потоковые шифры. Уже много лет человечество использует различные способы шифрования информации. Впрочем, на первых этапах

В случае если ключевая последовательность случайна и равна по длине шифруемому тексту, шифр взломать невозможно.

Нахождение k-error линейной сложности бинарной.

Ключевые слова: бинарная последовательность, линейная сложность, k-error линейная сложность, алгоритм Берлекэмпа — Мэсси, алгоритм Стэмпа и Мартина. Известно, что такое свойство последовательности, как линейная сложность.

Реализация алгоритма RC4 на CBuilder | Статья в журнале.

История. Потоковый шифр RC4 был создан Роном Ривестом из RSA Security в 1987 году.

Описание алгоритма. Рис. 1. Генератор ключевого потока RC4.

Эта функция генерирует последовательность битов (ki), которая затем объединяется с открытым текстом (mi).

Роль больших простых чисел в современной криптографии

Основные термины (генерируются автоматически): число, случайное число, простое число, случайная последовательность, работа алгоритма.

Генераторы случайных и псевдослучайных чисел.

Теория чисел в криптографии | Статья в журнале.

О случайности псевдослучайных последовательностей

число, случайное число, простое число, случайная последовательность, работа алгоритма, Равномерное распределение.

Последовательность , , . называется профилем линейной сложности последовательности. Методы генерации случайных чисел | Статья в журнале.

Исследование алгоритмов генерации простых чисел

Ключевые слова:вероятностный алгоритм, простые числа, псевдопростые числа, слабо псевдопростые числа, эффективность теста.

3. Найти большое случайное простое число. В этом случае мы тестируем различные случайные числа заданной сложности (под.

Обзор аппаратных генераторов случайных чисел

Ключевые слова: генератор случайных чисел, квантовый генератор, тепловой шум. Генераторы, использующие физические квантовые случайные процессы. Фазовый квантовый шум в лазерном луче.

Анализ псевдослучайных последовательностей на.

Статистической безопасностью: последовательность, созданная генератором псевдослучайных чисел должна статистически ничем не отличаться от абсолютно случайной последовательности.