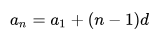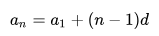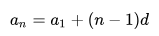Перый урок по теме «Арифметическая прогрессия» по учебнику Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова «Алгебра. 9 класс». учебник для общеобразовательных учреждений, под ред. С.А. Теляковского. –– М.: Просвещение, 2014 г.
Скачать:
| Вложение | Размер |
|---|---|
| arifmeticheskaya_progressiya.docx | 91.13 КБ |
| arifmeticheskaya_progressiya.pptx | 233.02 КБ |
Предварительный просмотр:
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ.
ФОРМУЛА (РЕКУРРЕНТНАЯ) п -го ЧЛЕНА АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ
— Расширить знания учащихся о последовательностях, ввести понятие арифметической прогрессии, формулу n-го члена арифметической прогрессии, её вывод.
— Способствовать воспитанию у учащихся логического мышления, внимания и аккуратности при применении формул n-го члена арифметической прогрессии. Вызвать интерес учащихся к математике.
— Способствовать формированию у учащихся:
умения анализировать математическое предложение;
умения выделять среди последовательностей арифметическую прогрессию;
умения записывать, выполнять вывод формулы n-го члена арифметической прогрессии и применять её при решении задач.
I. Организационный момент.
II. Актуализация знаний.
2-й б л о к. Актуализация знаний и создание проблемной ситуации.
Задать последовательность с помощью формулы п -го члена или рекуррентной формулы.
х 1 = –2; х п + 1 = х п + 2
х 1 = 2; х п + 1 = х п + 0,5
е) 0; 10; 20; 30; 40; …
х 1 = 0; х п + 1 = х п + 10
ж) а ; а + 3; а + 6; а + 9; …
х 1 = а ; х п + 1 = х п + 3
После заполнения таблицы анализируем полученные результаты и замечаем, что последовательности а), в), е) и ж) – одинакового вида, а именно: задаются рекуррентным способом и каждый член, начиная со второго, получается прибавлением к предыдущему числа (2; 0,5; 10; 3).
Учащиеся «открыли» определенный вид последовательности. Следует сказать, что такие последовательности называются «арифметическая прогрессия», и попросить учащихся попробовать самостоятельно сформулировать определение такой прогрессии на основе выделенных ими характеристических свойств.
III. Объяснение нового материала.
1. Определение. Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
( а п ) – арифметическая прогрессия, если для любого п N выполняется условие а п + 1 = а п + d , где d – некоторое число. Число d называется «разностью арифметической прогрессии», так как из определения следует, что а п + 1 – а п = d .
Далее следует привести примеры арифметических прогрессий, причем следует варьировать значение d (положительные числа; отрицательные; нуль; дробные).
П р и м е р ы арифметических прогрессий:
1; 2; 3; 4; … (последовательные натуральные числа).
1; 3; 5; 6; … (последовательность положительных
–2; –4; –6; –8; –10; … (последовательность отрицательных
7; 7; 7; 7; … (постоянная последовательность).
Обращаем внимание, что если d > 0, то арифметическая прогрессия возрастающая, если d d = 0 – постоянная.
2. Итак, учащиеся знают, что для того чтобы найти любой член арифметической прогрессии (или задать ее), достаточно знать ее первый член и разность. Следует подвести их к мысли, что это очень трудоемко, например:
( а п ) – арифметическая прогрессия, где а 1 = 2, d = 27. Найти сотый член.
Пользуясь определением, нам нужно сделать 100 шагов. Это громоздко. Хотелось бы знать формулу для нахождения любого члена арифметической прогрессии только по первому члену, разности и порядковому номеру искомого члена.
Для вывода формулы пользуемся определением арифметической прогрессии:
а 3 = а 2 + d = ( а 1 + d ) + d = а 1 + 2 d
а 4 = а 3 + d = ( а 1 + 2 d ) + d = а 1 + 3 d
а 5 = а 4 + d = ( а 1 + 3 d ) + d = а 1 + 4 d
а 6 = … = а 1 + 5 d
– формула п -го члена
П р и м е р 1. ( с п ) – арифметическая прогрессия,
с 1 = 0,62, d = 0,24; с 50 –?
с 50 = с 1 + d (50 – 1) = 0,62 + 0,24 · 49 = 12,38.
Этот пример на «прямое» использование формулы п -го члена арифметической прогрессии.
П р и м е р 2. Выяснить, является ли число –122 членом арифметической прогрессии ( х п ):
При рассмотрении этого примера пояснить, что для решения надо доказать, что существует п N , при котором будет верна формула п -го члена:
–122 = 23 + ( п – 1) · (–5,8), где
–5,8 = 17,2 – 23 – разность арифметической прогрессии.
IV. Формирование умений и навыков.
Все задания, выполняемые учащимися на этом уроке, можно разбить на 3 типа:
1) На «узнавание» арифметической прогрессии, определение ее первого члена и разности.
2) На нахождение п -го члена арифметической прогрессии по определению и по формуле.
3) На запись формулы п -го члена по первому члену и разности, решение задач на «косвенное» использование формулы п -го члена (например, нахождение п ).
2. № 575 (а, б), № 576 (а, в, д). Самостоятельное решение с последующей проверкой.
№ 577. Решение у доски с объяснением.
В о п р о с ы у ч а щ и м с я:
– Что называется арифметической прогрессией?
– Как задается арифметическая прогрессия?
– Назовите формулу п -го члена арифметической прогрессии.
Домашнее задание: № 575 (в, г); № 578; № 592.
Предварительный просмотр:
Подписи к слайдам:
Математический диктант по теме : «Последовательности»
1) Запишите пять членов последовательности чисел, I вариант к ратных числу 3 II вариант к ратных числу 5
2) Является ли конечной или бесконечной последовательность чисел, I вариант которые являются делителями числа 120? II вариант к ратных числу 8?
3) Перечислите члены последовательности, заключенные между I вариант у 29 и у 32 II вариант х 33 и х 37
4) Последовательность задана формулой I вариант а п = 5 п + 2 Запишите, чему равен а 4 II вариант b n = n 2 – 4 Запишите, чему равен b 5
I вариант 5) Запишите последний член последовательности трехзначных нечётных чисел II вариант 5) Запишите последний член последовательности двухзначных чётных чисел
6) Выпишите первые пять членов последовательности ( а n ), если I вариант а 1 = 15 а п + 1 = а п – 4 II вариант а 1 = -5 а п + 1 = а п + 3
7) Последовательность задана условиями I вариант b 1 = 12 b n + 1 = — 4· , Найдите b 4 II вариант b 1 = 15 b n + 1 = — 3· , Найдите b 6
8) Последовательность задана формулой II вариант I вариант a n = Сколько членов этой последовательности больше 1 a n = Сколько членов этой последовательности больше 2
Арифметическая прогрессия, формула ( рекуррентная) n — го члена арифметической прогрессии
понятие арифметической прогрессии, умение её распознавать; формула n- го члена арифметической прогрессии. Самые известные последовательности — это арифметическая и геометрическая прогрессии; Их основные свойства предстоит изучить. Цель нашего урока целеполагание
Актуализация знаний и создание проблемной ситуации Организация и самоорганизация учащихся. Организация обратной связи Последовательность а) –2; 0; 2; 4; … б) –5; 5; –5; 5; … в) 2; 2,5; 3; 3,5; 4; … г) 1; 4; 9; 16; … д) 1; … е) 0; 10; 20; 30; 40; … ж) а; а + 3; а + 6; а + 9; … Формула х 1 = –2; х n + 1 = х n + 2 х n = (– 1) n · 5 х 1 = 2 ; х n + 1 = х n + 0,5 х n = n 2 х 1 = 1 ; х n + 1 = х 1 = 0; х n + 1 = х n + 10 х 1 = а; х n + 1 = х n + 3 Задать последовательность с помощью формулы n -го члена или рекуррентной формулы
Арифметическая прогрессия Организация и самоорганизация учащихся. Организация обратной связи Определение Арифметической прогрессией называется последовательность, каждый член которой , начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом Разность арифметической прогрессии: d = a n+1 – a n a n+1 = a n + d d > 0 – прогрессия возрастающая d Мне нравится
Рекуррентная формула арифметической прогрессии
Теоретические сведения
Арифметическая прогрессия
Геометрическая прогрессия
Арифметической прогрессией an называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом d (d — разность прогрессий)
Геометрической прогрессией bn называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и тоже число q (q — знаменатель прогрессии)
Формула n-ого члена




В арифметической прогрессии ( an ) a1 = -6, a2 = -8. Найдите двадцать второй член прогрессии.
По формуле n-ого члена:
Необходимо найти разность прогрессий:
Найдите пятый член геометрической прогрессии: -3; 6;.
1-й способ (с помощью формулы n -члена)
По формуле n-ого члена геометрической прогрессии:
а 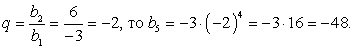
2-й способ (с помощью рекуррентной формулы)
Так как знаменатель прогрессии равен -2 ( q = -2), то:
В арифметической прогрессии ( an ) a74 = 34; a76 = 156. Найдите семьдесят пятый член этой прогрессии.
Для арифметической прогрессии характеристическое свойство имеет вид 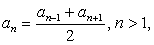 .
.
Из этого следует:
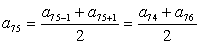 .
.
Подставим данные в формулу:
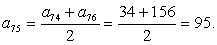
В арифметической прогрессии ( an ) an = 3 n — 4. Найдите сумму семнадцати первых членов.
Для нахождения суммы n-первых членов арифметической прогрессии используют две формулы:
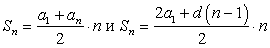 .
.
Какую из них в данном случае удобнее применять?
По условию известна формула n-ого члена исходной прогрессии ( an ) an = 3 n — 4. Можно найти сразу и a1 , и a16 без нахождения d . Поэтому воспользуемся первой формулой.
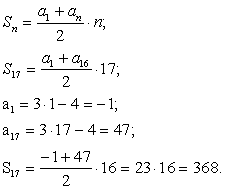
В арифметической прогрессии( an ) a1 = -6; a2 = -8. Найдите двадцать второй член прогрессии.
По формуле n-ого члена:
По условию, если a1 = -6, то a22 = -6 + 21 d . Необходимо найти разность прогрессий:
Записаны несколько последовательных членов геометрической прогрессии:
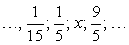
Найдите член прогрессии, обозначенный буквой x .
При решении воспользуемся формулой n-го члена bn = b1 ∙ q n — 1 для геометрических прогрессий. Первый член прогрессии. Чтобы найти знаменатель прогрессии q необходимо взять любой из данных членов прогрессии и разделить на предыдущий. В нашем примере можно взять и разделить на. Получим, что q = 3. Вместо n в формулу подставим 3, так как необходимо найти третий член, заданной геометрической прогрессии.
Подставив найденные значения в формулу, получим:
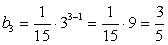 .
.
Ответ : 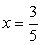 .
.
Из арифметических прогрессий, заданных формулой n-го члена, выберите ту, для которой выполняется условие a27 > 9:
1) 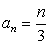 ;
;
2) 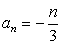 ;
;
3) 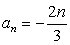 ;
;
4) 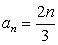 .
.
Так как заданное условие должно выполняться для 27-го члена прогрессии, подставим 27 вместо n в каждую из четырех прогрессий. В 4-й прогрессии получим:
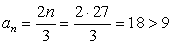 .
.
В арифметической прогрессии a1 = 3, d = -1,5. Укажите наибольшее значение n , для которого выполняется неравенство an > -6.
Воспользуемся формулой n-го члена.
Подставим данные в условии значения в формулу:
n Ответ : Наибольшее значение n = 6.
В геометрической прогрессии сумма первого и второго членов равна 108, а третьего и четвертого — 168,75. Найдите первых три члена прогрессии.
Составим систему уравнений:
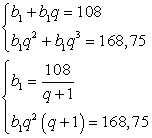
Подставим b1 во второе уравнение:
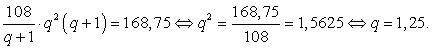
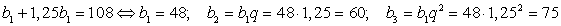 .
.
Произведение первого и пятого членов геометрической прогрессии равно 4, а частное от деления пятого члена на седьмой равно 9. Найдите четвертый член этой прогрессии.
Составим систему уравнений:
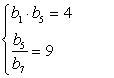
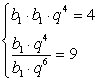
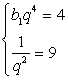
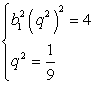
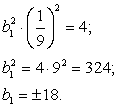
При 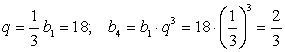 .
.
При 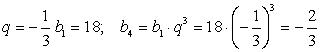 .
.
При 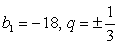 получим те же значения:
получим те же значения: 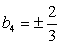 .
.
При 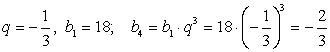 .
.
При 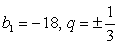 получим те же значения
получим те же значения 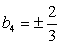 .
.
Арифметическая прогрессия
Разделы: Математика
Тип урока: объяснение нового материала.
Образовательные:
– выделить из множества числовых последовательностей арифметическую прогрессию;
– дать чёткое определение арифметической прогрессии;
– вывести формулу n-го члена прогрессии;
– описать характеристическое свойство арифметической прогрессии;
– на примерах осуществить первичную отработку применения формулы n-го члена арифметической прогрессии.
Воспитательные и развивающие:
– развивать логическое и аналитическое мышление;
– память;
– развитие и осмысление использования в речи математических терминов при ответах на вопросы теории алгебры.
Ход урока
1. Оргмомент :
Учитель сообщает тему и цель урока, план работы на уроке.
2. Устная работа
На доске: Учитель задает вопросы:
1) -4; -3,5; -3; … 1)Какая закономерность наблюдается
2) 2; 0,2; 0,02;… в каждой последовательности?
3) 7; 71/3; 72/3;… 2) Найдите последующий 4-ый и 5-ый члены
4)120; 117; 114;… каждой из числовых последовательностей.
3)А можно ли из данных пяти последовательностей выделить группу числовых рядов, объединённых каким-либо общем признаком?
3. Объяснение нового материала
Учитель подводит ученика к определению :
Арифметической прогрессией называют такую числовую последовательность, в которой каждый последующий член равен предыдущему, сложенным с одним и тем же числом.
Слово прогрессия в переводе с латинского означает “движение вперед”.
Число, которое прибавляют к каждому члену прогрессии, что бы найти последующий член называется разностью арифметической прогрессии
Найти разность арифметической прогрорессии: (устно) на доске :
| 4,5; 4,25; … | Учитель комментирует: | ||||||||||||||||||||||||||
| -6; -10; -14; … | d-может быть любым числом; | ||||||||||||||||||||||||||
| а1; а2; 30; 40; … | если d>0, прогрессия возрастающая; | ||||||||||||||||||||||||||
| 8; 8; 8; 8; … | если d число 295 не является членом этой арифметической прогрессии.
Приведём примеры числовых последовательностей, которые являются арифметическими прогрессиями: Учитель работает устно с классом: – ряд натуральных чисел; – кратных 10 и т.д. Запишем арифметическую прогрессию,которая представляет ряд чисел(натуральных) кратных 5 и арифметическую прогрессию заданную Тогда возвращаясь к a31 a31=a1+d*30 a31=2+0,4*30=14 Число :»А по какой формуле вы найдёте a41;a125;a207-? № 348(б) К доске вызывается ученик.
Учитель: Вернёмся к формуле n-ого члена арифметической прогрессии и проанализируйте её. Часто с формулами вы работаете на уроках и знаете что из одной формулы можно выразить любую неизвестную (в данной задаче) величину,зная все остальные переменные. Аналогично и по формуле нахождения n-ого члена прогрессии можно найти -n; Если известны остальные переменные. a1=20;a20=5;d-? Рассмотрим любые три подряд следующие члены прогрессий. Вопрос: «А как бы вы могли найти средний из этих трёх чисел,зная последующий и предыдущий? число 25(зная 20 и 30) число 11(зная 8 и 14)» Ответ: Сложить два соседних и разделить на два. А как называется значение этого выражения? – Это среднее арифметическое между 2-мя соседними. А верно ли это для любой арифметической прогрессии? Попробуем доказать это свойство, характерное для любой арифметической прогрессии. Пусть an-1;an;an+1-три любые подряд члена арифметической прогрессии an Запишем разность d с помощью этих членов an+1-an=an-an-1 an+1+an-1=2an an=(an+1+an-1/2),n>=2 Эта формула выражает характеристическое свойство арифметической прогрессии. Каждый член арифметической прогрессии, начиная со 2-ого члена является средним арифметическим между двумя соседними с ним членами. Почему начиная со 2-ого члена: так как у 1-ого члена прогрессии нет предыдущего члена. Верно и обратное утверждение: Если в числовой последовательности любой член, начиная со второго, является средним арифметическим между двумя соседними, то эта последовательность является арифметической прогрессией. То есть данное утверждение можно рассматривать как признак арифметической прогрессии. Найти: a19, если a20=120; a18=80 a19=(120+80/2)=100 Учащиеся устно находят a19 используя основное свойство прогрессии. Последнее задание: a8=40; a28=320 Учитель вместе с учащимися анализирует условие задачи(и да ),находит,что воспользоваться формулой для нахождения d в данном задании не приведёт к решению. Следовательно нужно искать иной способ решения. Рассмотрим арифметическую прогрессию(an),в которой известны ak,an,где k>n Запишем формулу каждого члена арифметической прогрессии: ak=a1+d(k-1);an=a1+d(n-1) ak-an=a1+d(k-1)-a1-d(n-1)=a1+dk-d-a1-dn+d=dk-dn=d(k-n) ak-an=d(k-n) или d=(ak-an/k-n) или ak=an-d(k-n) Эта формула выражает связь между двумя любыми членами арифметической прогрессии (следующими не подряд,и среды пятерых нет a1. Тогда предложенная задача решается просто при использовании выведенной формулы: d=a28-a8/10; d=340-40/20=14. 5. Итог урока: учитель работает фронтально с классом, задавая вопросы по объяснённому материалу.Учитель оценивает учащихся, отвечающих у доски и активно с места. Арифметическая (алгебраическая) прогрессия определение, примеры нахождения с решением Часто, при решении задач, связанных с наблюдениями и присвоением значения определенному событию за определенный промежуток времени, получается ряд чисел, который именуется арифметической прогрессией. Одна из главных отличительных особенностей такая математическая модель имеет закономерность, по которой можно вычислить любой неизвестный член, что упрощает прогнозирование при вычислении физических ситуаций. Примерами повседневного использования могут являться наблюдение за температурой воздуха, прогнозирование расходов с занесением результатов в таблицу и др. Онлайн-калькулятор арифметической прогрессииОпределение и примеры арифметической прогрессииЭто последовательность из чисел, где каждое последующее число ряда (начиная со второго) увеличивается или уменьшается на определенную сумму, являющуюся константой. Кроме этого для описания используется ряд сопутствующих терминов и определений. Членом (аn) называется единичное число из последовательности. Разностью (d) называется фиксированное число, на которое увеличивается или уменьшается последующее число прогрессии. Кроме этого, существуют виды таких рядов:
В качестве примера представим последовательность чисел «3, 9, 15, 21, 27». Данный случай – этот ряд чисел попадает под характеристику арифметической прогрессии. Этот вывод делается в том случае, когда разница между членами ряда фиксирована и равняется 6. Виды арифметической (алгебраической) прогрессииРазновидности строятся на основании характеристики разности (d), а именно на основании отличия последней от нуля. Таким образом, можно встретить определенные вариации:
Если прогрессия не изменяется с каждым шагом на одну и ту же разность, то эта прогрессия непостоянная и арифметической не является. Важно знать: арифметическая от геометрической отличается тем, что в последней производится увеличение каждого последующего на один и тот же множитель. Формулы арифметической прогрессииОдно из важнейших свойств заключается в возможности вычисления любого числа конкретного места ряда. Чтобы решать это, необходима формула, показывающая, как находится член арифметической прогрессии. В общем виде она будет выглядеть, как значение предыдущего числа в ряду (an-1), к которому прибавляют разность (d): Также может возникнуть задача, когда надо просуммировать все числа ряда арифметической прогрессии (сумма членов). Если их малое количество, то можно посчитать это вручную, но если количество чисел перевалит за сотню, то проще будет воспользоваться специальной формулой для обработки. Итак, нам понадобится значение первого числа в ряду (a1) и последнего (an), а также информация об общем количестве чисел в ряду. Рекуррентная формула, показывающая, как искать сумму, будет выглядеть в таком случае следующим образом: Обратите внимание: под значением n подразумевается именно количество членов ряда, для которых производится нахождение суммы. Произведение членов арифметической прогрессии можно находить по похожей формуле: где, Pn – произведение, b1 и bn – соответственно первое и последнее числа, а n – количество членов. Отдельно следует коснуться такого понятия, как характеристическое свойство прогрессии. Оно сводится к выполнению определенного условия для каждого элемента: Примеры задач с решениемРассмотрим как решать задачи на заданную тему. Пример 1Требуется вычислить 574 член в ряду арифметической прогрессии, первые три члена которой «8, 15, 22…». Вариант рассуждений по примеру 1. Для нахождения любого конкретного элемента ряда нам необходима информация о значении первого члена (a1) и о разности (d). Чтобы вычислить разность, вычитаем из второго члена ряда первый (15 – Подставляя полученные значения, получим выражение вида a574 = 8 + (574-1) * 7. После вычисления получаем ответ: a574 = 4019. Пример 2Требуется вычислить 544 член ряда, являющийся арифметической прогрессией, при условии, что 154-ый член равен 17, а разность (d) равна 8. Вариант рассуждений по примеру 2. Пользоваться в данной ситуации мы будем формулой из предыдущего примера: Подставляя известные значения, получаем выражение – а544 = 17 + (544 1) * 8. Вычисляя, получаем ответ а544 = 4361. Пример 3Для подготовки к экзамену по биологии студенту Смирнову необходимо выучить 730 вопросов (включая загадки). Известно, что он весьма обеспокоен и по мере приближения даты экзамена учит ежедневно на 27 вопросов больше, чем в предыдущий день. Друг Смирнова выяснил, что тот в первый день выучил всего 17 вопросов. Требуется выяснить, сколько времени у студента ушло на подготовку. Вариант рассуждений по примеру 3. Очевидно, что случай с подготовкой студента к экзамену решается через формулы арифметической прогрессией (поскольку присутствует фиксированная разность d = 17). Производим подстановку известных данных: После подстановки получаем выражение: 730 = 17 + (n 1) * 27. После вычислений определяем ответ – 27 дней. Арифметическая прогрессия является наиболее простой из всех числовых зависимостей. Использование описанных формул позволит намного ускорить вычисления в задачах, где это требуется. Кроме этого, для упрощения можно использовать онлайн калькулятор. В школе данную тему изучают в программе за 9 класс, а основные задания касаются нахождения членов и сумм. Арифметическая прогрессияАрифметической прогрессией называют числовую последовательность, каждый следующий член которой получается из предыдущего прибавлением к нему постоянного числа. Это число называют разностью арифметической прогрессии и обозначают буквой (d).Например, последовательность (2); (5); (8); (11); (14)… является арифметической прогрессией, потому что каждый следующий элемент отличается от предыдущего на три (может быть получен из предыдущего прибавлением тройки):
В этой прогрессии разность (d) положительна (равна (3)), и поэтому каждый следующий член больше предыдущего. Такие прогрессии называются возрастающими. Однако (d) может быть и отрицательным числом. Например, в арифметической прогрессии (16); (10); (4); (-2); (-8)… разность прогрессии (d) равна минус шести.
И в этом случае каждый следующий элемент будет меньше, чем предыдущий. Эти прогрессии называются убывающими. Обозначение арифметической прогрессииПрогрессию обозначают маленькой латинской буквой.Числа, образующие прогрессию, называют ее членами (или элементами). Их обозначают той же буквой что и арифметическую прогрессию, но с числовым индексом, равным номеру элемента по порядку. Например, арифметическая прогрессия (a_n = left< 2; 5; 8; 11; 14…right>) состоит из элементов (a_1=2); (a_2=5); (a_3=8) и так далее. Иными словами, для прогрессии (a_n = left<2; 5; 8; 11; 14…right>)
Решение задач на арифметическую прогрессиюВ принципе, изложенной выше информации уже достаточно, чтобы решать практически любую задачу на арифметическую прогрессию (в том числе из тех, что предлагают на ОГЭ). Пример (ОГЭ). Арифметическая прогрессия задана условиями (b_1=7; d=4). Найдите (b_5).
В этой задаче нам дано начало цепочки (первый элемент) и шаг (разность). Зная их, мы легко можем восстановить прогрессию до любого нужного нам члена (в нашем случае – пятого).
Вот и все. Нужное нам значение найдено. Пример (ОГЭ). Даны первые три члена арифметической прогрессии: (62; 49; 36…) Найдите значение первого отрицательного члена этой прогрессии..
Нам даны первые элементы последовательности и известно, что она – арифметическая прогрессия. То есть, каждый элемент отличается от соседнего на одно и то же число. Узнаем на какое, вычтя из следующего элемента предыдущий: (d=49-62=-13).
Теперь мы можем восстановить нашу прогрессию до нужного нам (первого отрицательного) элемента.
Готово. Можно писать ответ. Пример (ОГЭ). Даны несколько идущих подряд элементов арифметической прогрессии: (…5; x; 10; 12,5. ) Найдите значение элемента, обозначенного буквой (x).
Чтоб найти (x), нам нужно знать на сколько следующий элемент отличается от предыдущего, иначе говоря – разность прогрессии. Найдем ее из двух известных соседних элементов: (d=12,5-10=2,5). А сейчас без проблем находим искомое: (x=5+2,5=7,5).
Готово. Можно писать ответ. Пример (ОГЭ). Арифметическая прогрессия задана следующими условиями: (a_1=-11); (a_
Нам нужно найти сумму первых шести членов прогрессии. Но мы не знаем их значений, нам дан только первый элемент. Поэтому сначала вычисляем значения по очереди, используя данное нам рекуррентное соотношение : (n=1); (a_<1+1>=a_1+5=-11+5=-6) Искомая сумма найдена. Пример (ОГЭ).В арифметической прогрессии (a_<12>=23); (a_<16>=51). Найдите разность этой прогрессии.
| Мы знаем (12)-ый и (16)-ый элементы – и больше ничего. Однако этого достаточно для того, чтобы найти разность. Нужно просто посмотреть на схему слева и понять, что мы можем получить (16)-ый элемент из (12)-го, «сделав 4 шага», то есть четыре раза прибавив разность прогрессии. Иными словами: (a_<12>+d+d+d+d=a_<16>). | |||||||||||||||||||||||||

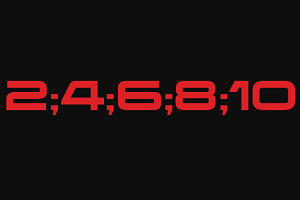
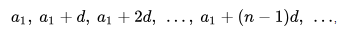


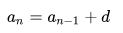
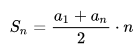
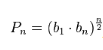
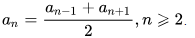
 и получаем d = 7. Теперь мы можем считать по формуле:
и получаем d = 7. Теперь мы можем считать по формуле: