Описательная статистика Excel позволяет за несколько минут обработать достаточно большое количество информации и найти необходимые значения, учитывая определенный набор условий и критерий. Обработка данных большого ряда значений согласно всем законам статистики – нет проблем, Microsoft Excel справиться со всем.
Для того чтобы сформировать вывод о результатах полученных данных с целого ряда массива значений можно использовать достаточно простую функцию из «Пакета анализа», которая позволит систематизировать эмпирические значения согласно определенным критериям.
Эта функция можем высчитывать большинство критериев, среди которых:
• Отклонение и стандартное отклонение;
• Ошибка и стандартная ошибка;
• Асимметричность значений;
• Мода;
• Дисперсия;
• Медиана;
• Другие значения.
По умолчанию, возможность работы с «Относительной статистикой» скрыта от большинства пользователей. Для того чтобы активировать данную панель, необходимо включить ее в параметрах документа.
Для этого нажмем на вкладку «Файл» — «Параметры».
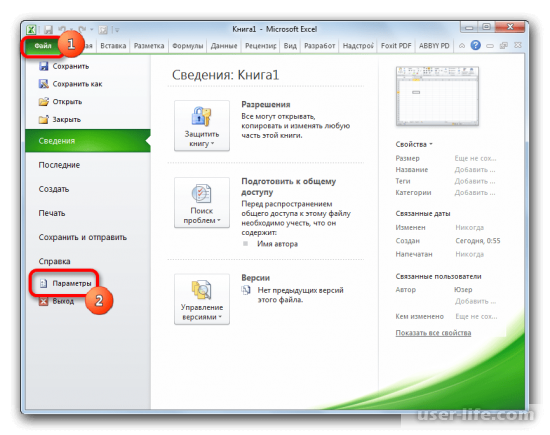
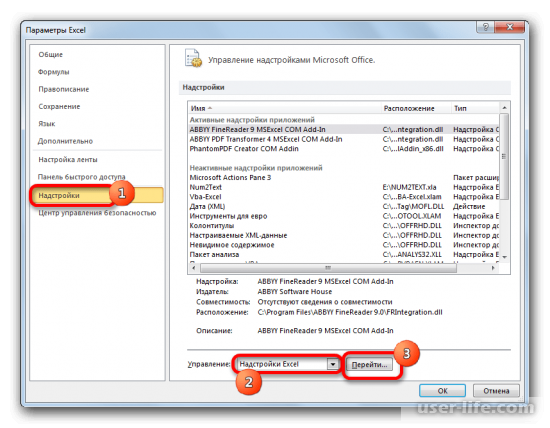
В появившемся диалоговом окне перейдем в меню «Надстройки», где внизу в подменю «Управление» нужно выбрать «Надстройки Excel» и перейти к последующим настройкам.
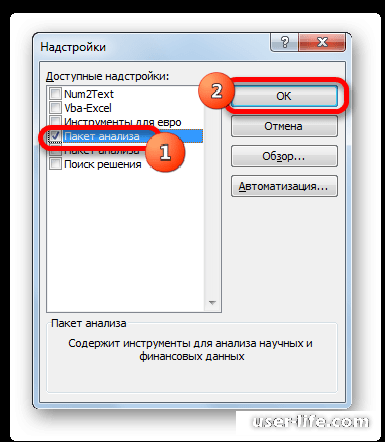
В новом окне ставим галочку напротив «Пакет анализа» и применяем операцию.
Весь функционал «Пакета анализа» был добавлен в рабочую область и появился во вкладке «Данные». Приступим непосредственно к «Описательной статистике» и попробуем на практике данный инструмент.
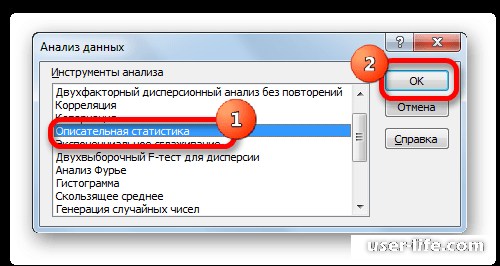
Перейдем во вкладку «Анализ данных», которая размещена в «Данных» и выбираем функцию «Описательная статистика».
Теперь необходимо заполнить все поля и ввести аргументы функции.
• «Входной интервал» — укажем весь диапазон данных, для которых необходимо применить функцию «Описательной статистики» — выделяем весь столбец вместе с названием с включением функции «Метки в первой строке».
• Включим группирование «По строкам» и «По столбцам».
• Выберем место, куда будут сохраняться результаты работы функции, это могут быть и новая книга, новый лист либо просто выбранный интервал.
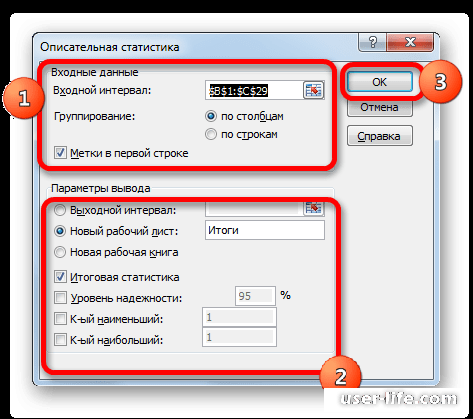
Теперь можно анализировать результаты работы функции. «Описательная статистика» рассчитала сразу несколько показателей, которые дают более четкое представление о выполненной работе: интервал, минимум и максимум, общую сумму и среднее значение и так далее.
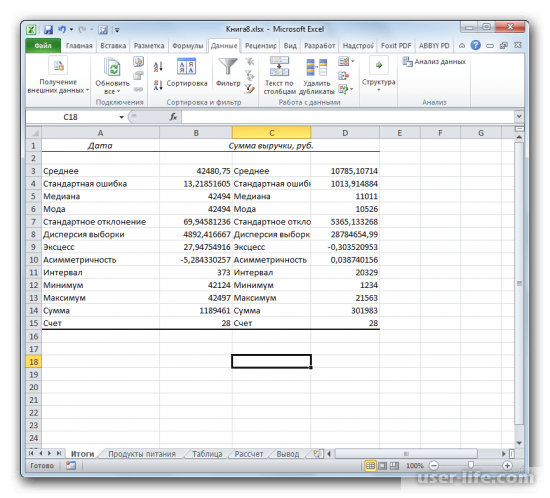
Пакет анализа предлагает пользователю результаты сразу по нескольким критериям. Это экономит большое количество времени, которое ушло бы на отдельный расчет по каждому показателю.
Описательная статистика в excel
Инструмент Описательная статистика входит в Пакет анализа (активация Пакета анализа смотри п.2.7.2). С его помощью можно в очень короткие сроки, использовав ресурсы программы, обработать массив данных и получить о нем информацию по целому ряду статистических критериев. Среди критериев, которые высчитывает данный инструмент следующие показатели:
- Медиана;
- Мода;
- Дисперсия;
- Среднее;
- Стандартное отклонение;
- Стандартная ошибка;
- Асимметричность и др.
Рассмотрим работу данного инструмента на примере задачи 4.2.
Переходим во вкладку «Данные» и выполняем щелчок по кнопке «Анализ данных», которая размещена на ленте в блоке инструментов «Анализ». Открывается список инструментов, представленных в Пакете анализа. Ищем наименование «Описательная статистика», выделяем его и щелкаем по кнопке «OK» (рис. 4.1).
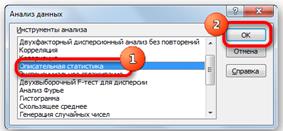 |
| Рис. 4.1. Описательная статистика |
После выполнения данных действий непосредственно запускается окно «Описательная статистика».
В поле «Входной интервал» указываем адрес диапазона, который будет подвергаться обработке этим инструментом. Причем указываем его вместе с шапкой таблицы. Так как мы захватили данные вместе с шапкой, то около параметра «Метки в первой строке» следует установить флажок. Тут же выбираем тип группирования, переставив переключатель в позицию «По столбцам» или «По строкам». В нашем случае подходит вариант «По столбцам», но в других случаях, возможно, придется выставить переключатель иначе.
Выше мы говорили исключительно о входных данных. Теперь переходим к разбору настроек параметров вывода, которые расположены в этом же окне формирования описательной статистики. Прежде всего, нам нужно определиться, куда именно будут выводиться обработанные данные:
- Выходной интервал;
- Новый рабочий лист;
- Новая рабочая книга.
В первом случае нужно указать конкретный диапазон на текущем листе или его верхнюю левую ячейку, куда будет выводиться обработанная информация. Во втором случае следует указать название конкретного листа данной книги, где будет отображаться результат обработки. Если листа с таким наименованием в данный момент нет, то он будет создан автоматически после того, как вы нажмете на кнопку «OK». В третьем случае никаких дополнительных параметров указывать не нужно, так как данные будут выводиться в отдельном файле Excel (книге). Мы выбираем вывод результатов на этом же рабочем листе (рис.4.2).
Далее, если вы хотите чтобы выводилась также итоговая статистика, то нужно установить флажок около соответствующего пункта. Также можно установить уровень надежности, поставив галочку около соответствующего значения. По умолчанию он будет равен 95%, но его можно изменить, внеся другие числа в поле справа.
Кроме этого, можно установить галочки в пунктах «K-ый наименьший» и «K-ый наибольший», установив значения в соответствующих полях. Этот параметр, также как и предыдущий, не является обязательным, поэтому флажки можно не ставить.
После того, как все указанные данные внесены, жмем на кнопку «OK».
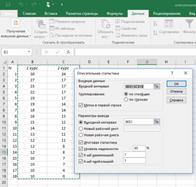 |
| Рис. 4.2. Параметры инструмента Описательная статистика |
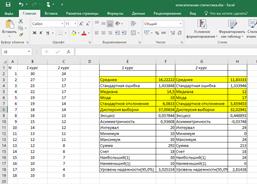 |
| Рис.4.3. Результаты, полученные с помощью Описательной статистики |
Среди множества показателей Описательной статистики есть те, которые нас интересуют, они выделены цветом (рис. 4.3).
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Дайте определение размаху, выборочной дисперсии, генеральной дисперсии, стандартному отклонению. Воспроизведите формулы для их нахождения.
2. Что характеризует выборочная дисперсия.
3. Вычислите для множества: 22, 15, 16, 21, 24, 24, 27, 28, 30, 30, 31, 31, 31, 34, 36 размах, дисперсию, стандартное отклонение.
4. В каких случаях можно проводить сравнение разных выборок по дисперсиям?
5. Выборочные дисперсии результатов контрольной работы в классе 7«А» и 7«Б» соответственно равны 0,44 и 1,38. Какой вывод можно сделать при сравнении результатов контрольной работы в двух классах?
6. Дисперсия каждой из групп A и В равна 5. Будет ли дисперсия 10 значений, полученных путем объединения групп, меньше, больше или равна 5?
Группа А: 13, 11, 10, 9, 7
Группа В: 28, 26, 25, 24, 22
Лабораторная работа №2
Описательная статистика
Этапы обработки данных:
1. Занести данные в таблицу Excel (две выборки).
2. Упорядочить данные (по возрастанию) в каждой выборке.
3. Рассчитать моду, медиану и среднее.
4. Посчитать дисперсию, стандартное отклонение.
5. Посчитать коэффициент вариации.
6. Сделать сравнительный анализ, полученных результатов.
Задания для вариантов 1 – 5
При определении степени выраженности некоторого психического свойства в двух группах, опытной и контрольной, баллы распределились следующим образом.
Дать сравнительную характеристику степени выраженности этого свойства в данных группах.
Вариант 1.
| Опытная | 18, 15, 16, 11, 14,15, 16, 16, 20, 22, 17, 12, 11, 12, 18, 19, 20 |
| Контрольная | 26, 8, 11, 12, 25, 22, 13, 14, 21, 20, 15, 16, 17, 16, 9, 11, 16 |
Вариант 2
| Опытная | 19, 16, 17, 12, 15,16, 17,17, 21, 23, 18, 13, 12, 13, 19, 20, 21 |
| Контрольная | 27, 9, 12, 13, 26, 23, 14, 15, 22, 21, 16, 16, 18, 17, 10, 12, 17 |
Вариант 3.
| Опытная | 16, 13, 14, 9, 10,13, 14,14, 18, 20, 15, 10, 9, 10, 16, 17, 18 |
| Контрольная | 24, 6, 9, 10, 23, 20, 11, 12, 19, 18, 13, 14, 12, 14, 7, 9, 14 |
| Опытная | 15, 12, 13, 8, 11,12, 13,13, 17, 19, 14, 9, 8, 9, 15, 16, 17 |
| Контрольная | 23, 5, 9, 9, 22, 19, 10, 11, 18, 17, 12, 13, 14, 13, 6, 8, 13 |
| Опытная | 15, 12, 13, 8, 11,12, 13,13, 17, 19, 14, 9, 8, 9, 15, 16, 17 |
| Контрольная | 24, 6, 9, 10, 23, 20, 11, 12, 19, 18, 13, 14, 12, 14, 7, 9, 14 |
Задания для вариантов 6 – 10
Была исследована группа детей с заболеванием крови до лечения препаратами и после лечения. В таблицу занесены показатели крови по результатам медицинского обследования. Сделать сравнительный анализ результативности лечения данным препаратом, используя методы описательной статистики.
| до лечения | 20,5 12,1 13,6 40,5 9,6 33 77,2 8,7 3,5 13,8 7,4 29,4 116 21,9 |
| после лечения | 2,3 7,5 3,8 3,8 8,8 13 4,7 3,9 4,8 5,7 9 13 0,9 |
| до лечения | 280 230 100 60 90 80 8 36 50 90 17 42 42 30 |
| после лечения | 86 280 30 170 210 230 230 156 102 161 15 60 20 |
| до лечения | 112 60 84 60 60 40 76 60 84 40 112 46 64 70 |
| после лечения | 82 78 110 130 130 104 108 129 110 88 105 73 85 80 |
| до лечения | 113 61 85 61 61 41 77 61 85 41 113 47 65 71 |
| после лечения | 81 77 109 129 129 103 107 128 109 87 104 72 84 79 |
| до лечения | 111 59 83 59 59 39 75 59 83 39 111 45 63 69 |
| после лечения | 83 79 111 131 131 105 109 130 111 89 106 74 86 81 |
Задания для вариантов 11 – 15
Для проверки эффективности новой развивающей программы были созданы две группы детей шестилетнего возраста. На первом этапе дети обеих групп были протестированы по методике Керна-Йерасика (школьная зрелость). Результаты тестирования по невербальной шкале занесены в таблицу. Сделать сравнительный анализ школьной зрелости детей этих групп.
| Эксперимент. | 29 31 31 25 25 19 22 20 14 16 27 24 32 27 14 24 |
| Контроль | 34 31 28 27 30 23 21 28 29 31 17 22 21 15 33 29 |
| Эксперимент. | 14 13 11 8 12 13 13 13 11 12 14 13 12 14 10 13 |
| Контроль | 13 13 14 12 14 14 12 13 15 13 11 12 14 9 14 13 |
| Эксперимент. | 33 33 37 33 34 33 31 29 29 35 31 29 31 34 26 26 |
| Контроль | 39 30 38 36 31 37 35 32 39 34 30 32 36 29 39 36 |
| Эксперимент. | 13 12 10 7 11 12 12 12 10 11 13 12 11 13 9 12 |
| Контроль | 12 12 13 11 13 13 11 12 14 12 10 11 13 8 13 12 |
| Эксперимент. | 30 32 32 26 26 20 23 21 15 17 28 25 33 28 15 25 |
| Контроль | 35 32 29 28 31 24 22 29 30 32 18 24 22 16 34 30 |
Задания для вариантов 16 – 20
У участников психологического исследования, в число которых входила группа педагогов и группа непедагогов, был исследован уровень конфликтности. Полученные данные занесены в таблицу. Можно ли утверждать, что уровень конфликтности педагогов выше, чем у непедагогов?
Использование пакета анализа
Если вам нужно провести сложный статистический или инженерный анализ, можно сэкономить время и этапы с помощью «Pak анализа». Вы предоставляете данные и параметры для каждого анализа, а средство использует соответствующие статистические или инженерные функции для вычисления и отображения результатов в выходной таблице. Некоторые средства создают диаграммы в дополнение к выходным таблицам.
Функции анализа данных можно применять только на одном листе. Если анализ данных проводится в группе, состоящей из нескольких листов, то результаты будут выведены на первом листе, на остальных листах будут выведены пустые диапазоны, содержащие только форматы. Чтобы провести анализ данных на всех листах, повторите процедуру для каждого листа в отдельности.
Ниже описаны инструменты, включенные в пакет анализа. Для доступа к ним нажмите кнопку Анализ данных в группе Анализ на вкладке Данные. Если команда Анализ данных недоступна, необходимо загрузить надстройку «Пакет анализа».
Откройте вкладку Файл, нажмите кнопку Параметры и выберите категорию Надстройки.
Если вы используете Excel 2007, нажмите Microsoft Office кнопку и выберите «Параметры Excel»
В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
Если вы используете Excel для Mac, в строке меню откройте вкладку Средства и в раскрывающемся списке выберите пункт Надстройки для Excel.
В диалоговом окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
Примечание: Чтобы включить Visual Basic для приложений (VBA) в надстройку «Надстройка «Анализ», можно загрузить его так же, как и надстройку «Надстройка «Анализ». В поле «Доступные надстройки» выберите «Надстройка анализа — VBA».
Существует несколько видов дисперсионного анализа. Нужный вариант выбирается с учетом числа факторов и имеющихся выборок из генеральной совокупности.
Однофакторный дисперсионный анализ
Этот инструмент выполняет простой анализ дисперсии данных для двух или более выборок. Анализ предоставляет проверку гипотезы о том, что все выборки взяты из одного и того же распределения вероятности относительно альтернативной гипотезы о том, что распределение вероятностей не одинаково для всех выборок. Если выборок всего два, можно использовать функцию T. ТЕСТ. В более чем двух примерах не существует удобного обобщения T. Ивместо нее можно использовать модель однофакторного коэффициента.
Двухфакторный дисперсионный анализ с повторениями
Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам. Например, в эксперименте по измерению высоты растений последние обрабатывали удобрениями от различных изготовителей (например, A, B, C) и содержали при различной температуре (например, низкой и высокой). Таким образом, для каждой из 6 возможных пар условий <удобрение, температура>, имеется одинаковый набор наблюдений за ростом растений. С помощью этого дисперсионного анализа можно проверить следующие гипотезы:
Извлечены ли данные о росте растений для различных марок удобрений из одной генеральной совокупности. Температура в этом анализе не учитывается.
Извлечены ли данные о росте растений для различных уровней температуры из одной генеральной совокупности. Марка удобрения в этом анализе не учитывается.
Извлечены ли шесть выборок, представляющих все пары значений <удобрение, температура>, используемые для оценки влияния различных марок удобрений (для первого пункта в списке) и уровней температуры (для второго пункта в списке), из одной генеральной совокупности. Альтернативная гипотеза предполагает, что влияние конкретных пар <удобрение, температура>превышает влияние отдельно удобрения и отдельно температуры.
Двухфакторный дисперсионный анализ без повторений
Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам, как в случае двухфакторного дисперсионного анализа с повторениями. Однако в таком анализе предполагается, что для каждой пары параметров есть только одно измерение (например, для каждой пары параметров <удобрение, температура>из предыдущего примера).
Функции КОРРЕЛ и PEARSON рассчитывают коэффициент корреляции между двумя переменными измерения, если измерения по каждой переменной наблюдались для каждого из N-объектов. (Отсутствуют результаты наблюдений по любой теме, которые при анализе игнорируются.) Инструмент анализа корреляции особенно удобен, если для каждого субъекта N существует более двух переменных измерения. Она содержит выходную таблицу — матрицу корреляции, которая показывает значение КОРРЕЛ (или PEARSON),примененного к каждой из возможных пар переменных измерения.
Коэффициент корреляции, как и ковариана, — это мера степени, в которой две переменные измерения «различаются». В отличие от ковариации коэффициент корреляции масштабирован таким образом, что его значение не зависит от единиц, в которых выражены две переменные измерения. (Например, если двумя переменными измерения являются вес и высота, коэффициент корреляции не изменяется, если вес преобразуется из фунта в фунты.) Значение любого коэффициента корреляции должно быть включительно (от -1 до +1).
Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, т. е. большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (нулевая корреляция).
Средства корреляции и ковариатора можно использовать в одном и том же параметре, если у вас есть N различных переменных измерения для набора людей. Каждый из инструментов корреляции и ковариции дает выходную таблицу — матрицу, в которую указывается коэффициент корреляции или коварианс между каждой парой переменных измерения. Разница заключается в том, что коэффициенты корреляции масштабироваться в зависимости от -1 и +1 включительно. Соответствующие ковариансии не масштабироваться. Коэффициент корреляции и ковариатор — это меры, в которых две переменные «различаются».
Инструмент «Ковариана» вычисляет значение функции КОВАРИАНАС на этом компьютере. P для каждой пары переменных измерения. (Непосредственное использование КОВАРИАНС. Вместо ковариатора P лучше использовать ковариативную единицу, если имеется только две переменных измерения, то есть N=2.) Запись на диагонали выходной таблицы инструмента «Ковариальная» в строке i, столбце i — ковариальная величина i-й переменной. Это только дисперсия по численности населения для этой переменной, вычисляемая функцией ДИСПЕ. P.
Ковариационный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть большие значения из одного набора данных связаны с большими значениями другого набора (положительная ковариация) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная ковариация), или данные двух диапазонов никак не связаны (ковариация близка к нулю).
Инструмент анализа «Описательная статистика» применяется для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.
Инструмент анализа «Экспоненциальное сглаживание» применяется для предсказания значения на основе прогноза для предыдущего периода, скорректированного с учетом погрешностей в этом прогнозе. При анализе используется константа сглаживания a, величина которой определяет степень влияния на прогнозы погрешностей в предыдущем прогнозе.
Примечание: Для константы сглаживания наиболее подходящими являются значения от 0,2 до 0,3. Эти значения показывают, что ошибка текущего прогноза установлена на уровне от 20 до 30 процентов ошибки предыдущего прогноза. Более высокие значения константы ускоряют отклик, но могут привести к непредсказуемым выбросам. Низкие значения константы могут привести к большим промежуткам между предсказанными значениями.
Двухвыборочный F-тест применяется для сравнения дисперсий двух генеральных совокупностей.
Например, можно использовать F-тест по выборкам результатов заплыва для каждой из двух команд. Это средство предоставляет результаты сравнения нулевой гипотезы о том, что эти две выборки взяты из распределения с равными дисперсиями, с гипотезой, предполагающей, что дисперсии различны в базовом распределении.
С помощью этого инструмента вычисляется значение f F-статистики (или F-коэффициент). Значение f, близкое к 1, показывает, что дисперсии генеральной совокупности равны. В таблице результатов, если f 1, «P(F
Инструмент «Анализ Фурье» применяется для решения задач в линейных системах и анализа периодических данных на основе метода быстрого преобразования Фурье (БПФ). Этот инструмент поддерживает также обратные преобразования, при этом инвертирование преобразованных данных возвращает исходные данные.
Инструмент «Гистограмма» применяется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. При этом рассчитываются числа попаданий для заданного диапазона ячеек.
Например, можно получить распределение успеваемости по шкале оценок в группе из 20 студентов. Таблица гистограммы состоит из границ шкалы оценок и групп студентов, уровень успеваемости которых находится между самой нижней границей и текущей границей. Наиболее часто встречающийся уровень является модой диапазона данных.
Совет: В Excel 2016 теперь можно создавать гистограммы и диаграммы Парето.
Инструмент анализа «Скользящее среднее» применяется для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного числа предшествующих периодов. Скользящее среднее, в отличие от простого среднего для всей выборки, содержит сведения о тенденциях изменения данных. Этот метод может использоваться для прогноза сбыта, запасов и других тенденций. Расчет прогнозируемых значений выполняется по следующей формуле:
N — число предшествующих периодов, входящих в скользящее среднее;
A j — фактическое значение в момент времени j;
F j — прогнозируемое значение в момент времени j.
Инструмент «Генерация случайных чисел» применяется для заполнения диапазона случайными числами, извлеченными из одного или нескольких распределений. С помощью этой процедуры можно моделировать объекты, имеющие случайную природу, по известному распределению вероятностей. Например, можно использовать нормальное распределение для моделирования совокупности данных по росту людей или использовать распределение Бернулли для двух вероятных исходов, чтобы описать совокупность результатов бросания монеты.
Инструмент анализа «Ранг» и «Процентиль» создает таблицу, которая содержит порядкованный и процентный ранг каждого значения в наборе данных. Можно проанализировать относительное положение значений в наборе данных. В этом средстве используются функции РАНГ. EQ и PERCENTRANK. INC. Если вы хотите учитывать связанные значения, используйте РАНГ. Функция EQ, которая рассматривает связанные значения как связанные значения с одинаковым рангом, или использует РАНГ. Функция AVG, которая возвращает среднее ранг для связанных значений.
Инструмент анализа «Регрессия» применяется для подбора графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или нескольких независимых переменных. Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес. Можно вычислить степень влияния каждого из этих трех факторов по результатам выступления спортсмена, а затем использовать полученные данные для предсказания выступления другого спортсмена.
Инструмент «Регрессия» использует функцию LINEST.
Инструмент анализа «Выборка» создает выборку из генеральной совокупности, рассматривая входной диапазон как генеральную совокупность. Если совокупность слишком велика для обработки или построения диаграммы, можно использовать представительную выборку. Кроме того, если предполагается периодичность входных данных, то можно создать выборку, содержащую значения только из отдельной части цикла. Например, если входной диапазон содержит данные для квартальных продаж, создание выборки с периодом 4 разместит в выходном диапазоне значения продаж из одного и того же квартала.
Двухвыборочный t-тест проверяет равенство средних значений генеральной совокупности по каждой выборке. Три вида этого теста допускают следующие условия: равные дисперсии генерального распределения, дисперсии генеральной совокупности не равны, а также представление двух выборок до и после наблюдения по одному и тому же субъекту.
Для всех трех средств, перечисленных ниже, значение t вычисляется и отображается как «t-статистика» в выводимой таблице. В зависимости от данных это значение t может быть отрицательным или неотрицательным. Если предположить, что средние генеральной совокупности равны, при t =0 «P(T Парный двухвыборочный t-тест для средних
Парный тест используется, когда имеется естественная парность наблюдений в выборках, например, когда генеральная совокупность тестируется дважды — до и после эксперимента. Этот инструмент анализа применяется для проверки гипотезы о различии средних для двух выборок данных. В нем не предполагается равенство дисперсий генеральных совокупностей, из которых выбраны данные.
Примечание: Одним из результатов теста является совокупная дисперсия (совокупная мера распределения данных вокруг среднего значения), вычисляемая по следующей формуле:
Двухвыборочный t-тест с одинаковыми дисперсиями
Этот инструмент анализа выполняет двухуголовый t-тест учащегося. В этой форме t-теста предполагается, что два набора данных поступили из распределения с одинаковыми дисперсиями. Этот тест называется гомомоcedastic t-test. Этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами.
Двухвыборочный t-тест с различными дисперсиями
Этот инструмент анализа выполняет двухуголовый t-тест учащегося. В этой форме t-теста предполагается, что два набора данных поступили из распределений с неравными дисперсиями. Это называется гетероскестический t-тест. Как и в предыдущем случае с равными дисперсиями, этот t-тест можно использовать для определения вероятности того, что две выборки взяты из распределения с равными средствами. Этот тест можно использовать, если в двух примерах есть различные темы. Используйте парный тест, описанный в примере, если существует один набор субъектов и два примера представляют измерения для каждой темы до и после обработки.
Для определения тестовой величины t используется следующая формула.
Для вычисления степеней свободы (df) используется следующая формула: Так как результат вычисления обычно не является integer, значение df округлится до ближайшего ближайшего другого для получения критического значения из таблицы t. Функция листа Excel T. В этой проверке используется вычисляемая величина df без округления, так как ее можно вычислить для значения T. ТЕСТ с неинтегрным df. Из-за таких разных подходов к определению степеней свободы результаты T. Тест и этот t-тест различаются в случае неравных дисперсий.
Z-тест. Средство анализа «Две выборки для средств» выполняет два примера z-теста для средств со известными дисперсиями. Это средство используется для проверки гипотезы null о том, что между двумя значениями населения нет различий между односторонними или двухбокльными гипотезами. Если дисперсии не известны, функция Z. Вместо нее следует использовать тест.
При использовании этого инструмента следует внимательно просматривать результат. «P(Z = ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. «P(Z = ABS(z) или Z
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community, попросить помощи в сообществе Answers community, а также предложить новую функцию или улучшение на веб-сайте Excel User Voice.
ОПИСАТЕЛЬНАЯ СТАТИСТИКА
Первичный анализ скалярных экспериментальных данных начинается с вычисления описательных статистик. Добавив к этому графические характеристики, получим некоторые основания для выводов о характере распределения данных исследуемой совокупности. К тому же базовый анализ дает основу для дальнейшего проведения более сложного анализа данных.
Из множества инструментов надстройки «Анализ данных» будем использовать «Описательную статистику» для получения числовых характеристик и «Гистограмму» — для графических. Заметим, что наряду с этим можно использовать также встроенные «Статистические функции», которые дублируют возможности надстройки.
Рассмотрим работу с описательной статистикой на примере.
Пример 4.1. Имеются некоторые данные о стоимости новогодних туров (рис. 4.2). Каждый из столбцов можно рассматривать как отдельный признак или переменную. Требуется провести анализ данных о продолжительности туров.

Таблица исходных данных
Исходные данные содержат несколько переменных, характеризующих тур. «Название фирмы», «Страна», «Транспорт» — качественные переменные, которые относятся к номинальной шкале. «Отель» —качественная переменная, которую можно отнести к порядковой шкале, так как количество звездочек отражает уровень обслуживания в отеле. «Количество дней» и «Стоимость» —количественные данные, которые относятся к метрической шкале.
Вычислим основные описательные статистики для переменной «Количество дней», которая является числовой переменной, принимающей дискретные значения. Для этого используем инструмент «Описательная статистика», входящий в «Пакет анализа».
Для перехода к описательной статистике выполните: «Данные» —» «Анализ» —> «Анализ данных» —» «Описательная статистика» -> «Ок». В открывшемся диалоговом окне «Описательная статистика» (рис. 4.3) укажите «Входной интервал», диапазон В2:Б16, выберите «Труп-

Диалоговое окно «Описательной статистики»
иирование по столбцам», установите «Метки в первой строке», так как входной интервал содержит наименование столбца. Для «Выходного интервала» достаточно указать одну, первую, ячейку на текущем листе, как альтернативу можно выбрать «Новый рабочий лист» или «Новую рабочую книгу». И наконец, укажите хотя бы одну из выводимых статистик: «Итоговая статистика», «Уровень надежности», «К-й наименьший», «К-й наибольший».
В большинстве случаев достаточно выбрать «Итоговую статистику», которая рассчитывает основные числовые характеристики исследуемой совокупности. Три последних значения рассчитывают, только когда они действительно нужны.
«Описательная статистика» вычисляет 16 значений, из них 13 относятся к «Итоговой статистике», еще три определяют доверительный интервал и два выборочных значения.
Отметим главное — «Описательная статистка» надстройки «Анализ данных» предназначена для вычислений статистических характеристик, или статистик, одномерной выборки или нескольких выборок.
В литературе по статистике часто используют термин «генеральная совокупность». Обычно имеется в виду, что это множество всех доступных для наблюдения данных в противоположность «выборки» — которая подразумевает, что исследуется лишь часть данных выбранных из генеральной совокупности (может быть с помощью случайного отбора).
Обычно числовые характеристики генеральной совокупности называют параметрами, а числовые характеристики выборки — статистиками, или выборочными характеристиками, которые являются оценками параметров генеральной совокупности. Для более полного понимания выборочного метода следует обратиться к специальной литературе.
Результаты расчетов «Итоговой статистики» для переменной «Количество дней» приведены на рисунке 4.4. На этом же рисунке приведены альтернативные расчеты этих числовых характеристик с использованием встроенных функций категории «Статистические». Аргументом статистических функций является диапазон исходных данных, в данном случае D3:D16.
Таким образом, практически все расчеты «Описательной статистики» дублируются «Статистическими» функциями. Остальные характеристики можно посчитать, используя формулы. Для того чтобы на рабочем листе Excel отобразились не результаты, а формулы, следует выполнить: «Формулы» -» «Зависимости формул» -» «Показать формулы».
Отметим некоторое отличие в применении инструментов «Анализа данных» и использовании статистических функций. При изменении значений исходных данных формулы пересчитываются, в то время как результаты, полученные с помощью инструментов «Анализа данных»,

«Итоговая статистика» и «Статистические функции»
не изменяются. Чтобы обновить результаты, потребуется вызывать «Анализ данных» снова.
Числовые характеристики «Итоговой статистики» описывают средние, вариацию и форму распределения, всего 13 параметров:
- • среднее, или выборочное среднее, вычисляется как среднее арифметическое наблюдаемых значений выборки;
- • медиана определяется как значение, находящееся в середине распределения, полученного из исходного путем упорядочивания по возрастанию;
- • мода равна наиболее часто встречающемуся значению. Кроме того, выделяют две величины, характеризующие изменчивость, или разброс, значений распределения относительно среднего:
- 1) дисперсию выборки, или выборочную дисперсию, равную сумме квадратов отклонений каждого значения от среднего, деленной на (А — 1), где N — число значений в распределении, или объем выборки;
2) стандартное отклонение, или выборочное среднеквадратическое отклонение, равное квадратному корню из выборочной дисперсии.
Дополнительными мерами изменчивости являются три простые характеристики, отражающие границы распределения данных и его размах:
- • минимум равен наименьшему из выборочных значений;
- • максимум равен наибольшему из выборочных значений;
- • интервал составляет разность между максимумом и
минимумом, этот параметр называют также размахом.
Если набор данных рассматривается как множество
независимых реализаций случайной величины, то возникает вопрос, что можно сказать о функции распределения этой величины на основании выборки. Очень часто распределение оказывается нормальным или близким к нему.
Для отражения близости формы распределения к нормальному виду существует две основные характеристики:
- 1) эксцесс, или выборочный коэффициент эксцесса, который является мерой «сглаженности» распределения;
- 2) асимметричность, или выборочный коэффициент асимметрии, показывает, в какую сторону относительно среднего сдвинуто большинство значений выборки.
И наконец, сумма равна сумме всех выборочных значений, счет вычисляет объем выборки, стандартная ошибка равна выборочному стандартному отклонению, деленному на квадратный корень из объема выборки.
При необходимости можно вычислить три дополнительные характеристики (рис. 4.5). Результаты расчетов этих характеристик приведены на рисунке 4.6.
«К-й наибольший» выдает К-е выборочное значение, если бы выборка была отсортирована по убыванию. В рассматриваемом примере сортировка по убыванию имеет вид 14,12,12,12, 11, Юит. д., третье значение равно 12. «К-й наименьший» выдает К-е выборочное значение, если бы выборка была отсортирована по возрастанию, это значение равно 5.
Задав «Уровень надежности», например 95%, получим значение для построения доверительного интервала для

Описательная статистика, дополнительные параметры

Результаты расчетов дополнительных параметров
неизвестного математического ожидания генеральной средней с доверительным уровнем 95%. Доверительный интервал строится как выборочное среднее плюс-минус полученное значение. Обратим внимание, что граница здесь вычисляется с помощью распределения Стьюдента, что требует достаточного количества наблюдений на каждую степень свободы.
Таким образом, к вычислению доверительных интервалов нужно относиться с осторожностью, особенно при малых выборках. Использование функции расчета доверительного интервала без понимания статистического смысла может привести к ошибкам. Начинающим исследователям посоветуем обратиться к специальной литературе.
Например, для рассматриваемого примера полученный доверительный интервал не несет смыслового содержания.
Итак, на этапе проведения описательной статистики исследуемый ряд данных может быть как генеральной совокупностью, так и выборкой. Если для генеральной совокупности вычисляются значения параметров распределения, то для выборки находят оценки этих параметров. Рассмотрим ниже подробнее вычисление некоторых числовых характеристик в пакете Excel.
Построение доверительных интервалов для среднего. Описательная статистика в Excel





ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3
Описательная статистика в Excel
Вычисление границ доверительных интервалов в Excel
Использование инструмента Пакета анализа Описательная статистика.
Построение доверительных интервалов для среднего.
В пакете Excel помимо мастера функций имеется набор более мощных инструментов для работы с несколькими выборками углубленного анализа данных, называемый Пакет анализа, который может быть использован для решения задач статистической обработки выборочных данных.
Для установки раздела Анализ данных в пакете Excel сделайте следующее:
— в меню Сервис выберите команду Надстройки;
— в появившемся списке установите флажок Пакет анализа.
Ввод данных. Исследуемые данные следует представить в виде таблицы, где столбцами являются соответствующие показатели. При создании таблицы Excel информация вводится в отдельные ячейки. Совокупность ячеек, содержащих анализируемые данные, называется входным диапазоном.
Последовательность обработки данных. Для использования статистического пакета анализа данных необходимо:
— указать курсором мыши на пункт меню Сервис и щелкнуть левой кнопкой мыши;
— в раскрывающемся списке выбрать команду Анализ данных (если команда Анализ данных отсутствует в меню Сервис, то необходимо установить в Excel пакет анализа данных);
— выбрать необходимую строку в появившемся списке Инструменты анализа;
— ввести входной и выходной диапазоны и выбрать необходимые параметры.
Нахождение основных выборочных характеристик. Для определения характеристик выборки используется процедура Описательная статистика. Процедура позволяет получить статистический отчет, содержащий информацию о центральной тенденции и изменчивости входных данных. Для выполнения процедуры необходимо:
— выполнить команду Сервис > Анализ данных;
— в появившемся списке Инструменты анализа выбрать строку Описательная статистика и нажать кнопку ОК (рис. 1);
— в появившемся диалоговом окне указать входной диапазон, то есть ввести ссылку на ячейки, содержащие анализируемые данные. Для этого следует навести указатель мыши на левую верхнюю ячейку данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;
Рис. 1. Окно выбора метода обработки данных
— указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной диапазон (навести указатель мыши и щелкнуть левой клавишей), далее навести указатель мыши в поле ввода Выходной диапазон и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши;
— в разделе Группировка переключатель установить в положение по столбцам; о установить флажок в поле Итоговая статистика;
— нажать кнопку ОК.
В результате анализа в указанном выходном диапазоне для каждого столбца данных выводятся следующие статистические характеристики: среднее, стандартная ошибка (среднего), медиана, мода, стандартное отклонение, дисперсия выборки, эксцесс, асимметричность, интервал, минимум, максимум, сумма, счет, наибольшее, наименьшее, уровень надежности.
Пример 1. Рассматривается зарплата основных групп работников гостиницы: администрации, обслуживающего персонала и работников ресторана. Были получены следующие данные:
Необходимо определить основные статистические характеристики в группах данных.
1. Для использования инструментов анализа исследуемые данные следует представить в виде таблицы, где столбцами являются соответствующие показатели. Значения зарплат сотрудников администрации введите в диапазон А1:А5, обслуживающего персонала— в диапазон В1:В8 и т. д. В результате получится таблица, представленная на рис. 2.

Рис. 2. Таблица из примера
2. Далее необходимо провести элементарную статистическую обработку. Для этого, указав курсором мыши на пункт меню Сервис, выберите команду Анализ данных. Затем в появившемся списке Инструменты анализа выберите строку Описательная статистика.
Рис. 3. Пример заполнения диалогового окна Описательная статистика
3. В появившемся диалоговом окне (рис. 3) в рабочем поле Входной интервал укажите входной диапазон —А1:С8. Активировав переключателем рабочее поле Выходной интервал, укажите выходной диапазон — ячейку А9. В разделе Группировка переключатель установите в положение по столбцам. Установите флажок в поле Итоговая статистика и нажмите кнопку ОК. В результате анализа (рис. 4) в указанном выходном диапазоне для каждого столбца данных получим соответствующие результаты.
Рис. 4. Результаты работы инструмента Описательная статистика.
1. Найдите наиболее популярный туристический маршрут из четырех реализуемых фирмой (моду), если за неделю последовательно были реализованы следующие маршруты (приводятся номера маршрутов): 1, 3, 3, 2, 1, 1, 4, 4, 2, 4, 1, 3, 2, 4, 1, 4, 4, 3, 1, 2, 3, 4, 1, 1, 3.
2. В рабочей зоне производились замеры концентрации вредного вещества. Получен ряд значений (в мг/м3): 12, 16, 15, 14, 10, 20, 16, 14, 18, 14, 15, 17, 23, 16. Необходимо определить основные выборочные характеристики.















