Учитель информатики
Информатика. 10 класса. Босова Л.Л. Оглавление
§13. Представление чисел в компьютере
Самым первым видом данных, с которыми начали работать компьютеры, были числа. ЭВМ первого поколения могли производить только математические расчёты (вычисления).
Из курса информатики основной школы вы помните, что компьютеры работают с целыми и вещественными числами. Их представление в памяти осуществляется разными способами.
Компьютер умеет применять к числу три операции
Микрокалькулятор МК-97 умеет над числами, занесенными в память, производить только три операции:
1) проверять, равны ли выбранные два числа,
2) складывать выбранные числа,
3) по выбранным числам a и b находить корни уравнения x² + ax + b = 0, а если корней нет, выдавать сообщение об этом.
Результаты всех действий заносятся в память. Первоначально в памяти записано одно число x. Как с помощью МК-97 узнать, равно ли это число единице?
Сложением x с самим собой получаем 2x. Сравниваем x и 2x. Если они равны, то x = 0. В противном случае ищем корни уравнения y² + 2xy + x = 0. Дискриминант этого уравнеия равен 4(x² – x), поэтому корни равны тогда и только тогда, когда x = 1.
Самостоятельная работа. Операции с целыми числами
1. Напишите логическую операцию и маску (в шестнадцатеричной системе счисления), которые нужно применить, чтобы ОБНУЛИТЬ указанные биты 16-битного целого числа (биты нумеруются справа налево, начиная с 0).
2. Напишите логическую операцию и маску (в шестнадцатеричной системе счисления), которые нужно применить, чтобы УСТАНОВИТЬ указанные биты 16-битного целого числа.
3. Выполните логическую операцию «исключающее ИЛИ» между заданными числами и запишите в ответе полученное число в шестнадцатеричной системе счисления.
4. Число записано в указанных битах 16-битного целого числа, хранящегося в переменной N. Какие операции нужно выполнить, чтобы записать это число в переменную X? Маски для выполнения логических операций записывайте в шестнадцатеричной системе счисления.
Входные данные: (пример)
3. 0x2E xor 0xC5
4. биты с 13 по 15
Давайте подробно разберем, как решаются такие задачи:
1. У нас есть какое-то число, которое занимает 16 бит. Нумеруются биты с «0». Поэтому нужно внимательно читать условие. Если говорится о позиции бита, то мы отсчитываем эту позицию справа налево, а если, как в нашей задаче, речь идет о «указанных битах», то мы просто выбираем биты с данными номерами.
 |
| х | х | х | х | х | х | х | х | х | х | х | х | х | х | х | х |

Само содержимое битов
У нас задача обнулить 2, 9 и 6 биты. Чтобы гарантированно получить ноль в этих позициях мы должны применить логическую операцию «И» с каким-то числом (это та самая маска), чтобы на выходе получилось число, отличающееся от первого только «0» в соответствующих битах.
| х | х | х | х | х | х | х | х | х | х | х | х | х | х | х | х |
Маска должна содержать «0» в 2, 6 и 9 битах, а все остальные значения вроде бы не важны. Но правильно применять так называемую строгую маску. Нам нужен гарантированно точный результат: что только в этих позициях будут производиться изменения. Поэтому маска будет представлять из себя число, где все биты будут равны «1», кроме 2,6 и 9. Там в маске должен стоять «0». И тогда, какое бы значение не пришло в этот бит регистра – на выходе мы всегда получим то, что хотели: «0»!
| х | х | х | х | х | х | х | х | х | х | х | х | х | х | х | х |
Дальше мы должны маску записать в 16-ном коде. Делается это элементарно: справа налево группируем по 4 бита и каждую такую группу переводим в 2-ную систему счисления. Если кому трудно это делать, то в винде есть программа «калькулятор», который в режиме «программист» осуществляет это легко и без ошибок. (На СР пользоваться им будет низзя.)
 0 0 |



Осталось сформулировать ответ: Операция «И» с маской FDBB
2. Второй вопрос разбирать я не вижу смысла. Там то же самое, только требование «установить 1» в какие-либо биты нужно понимать, как : операция «ИЛИ» с маской, где в заданных номерах битов будут «1» (Это 0, 3 и 4 в задании), а остальные заполняем «0».
3. Здесь требуется осуществить операцию «Исключающее ИЛИ» для двух заданных чисел. На что обратить внимание? 0х2Е – это один из видов записи числа в 16-ричной СС. Эти буковки говорят нам о том, что в самых младших 4-х разрядах регистра будет содержаться число Е (1110), в битах № 4-8 – число 2 (0010), а все, что осталось (старшие биты) – заполняем «0» .
Со вторым числом поступаем также, т.е. записываем и его в 2-ной СС в 16 битах. И выполняем операцию «xor» . Второе число выступает здесь в роли маски. Операция «исключающее или» работает просто и красиво: там, где в маске «0» значения битов первого числа не меняются, а где в маске стоит «1», биты первого числа инвертируются.
4. Ну, последнее задание в этой работе касается логического сдвига. Дано какое-то число, размер его 16 бит (переменная N). И в этом коде часть кода – тоже число, которое мы с вами должны выделить и записать в переменную Х. Нам указаны номера битов (13-15). Что мы делаем?
| х | х | х | n | n | n | n | n | n | n | n | n | n | n | n | n |
Будем использовать операцию «И» и маску такую, чтобы установить «0» везде, кроме указанных битов. Эта маска 0хЕ000: 1110 0000 0000 0000. Обратите внимание на то, что в записи 0хЕ000 старших битов, заполненных «0», нет. Все 16 разрядов заняты. Начинаем писать число всегда с младших разрядов! В таком случае 0хЕ000 просто указывает на то, что число 16-ричное.
Далее, мы сдвигаем число так, чтобы первая значимая единица установилась в младшем бите. Избавляемся от ненужных нулей ( прочитайте про выравнивание порядков и сдвиги – и просветление вам гарантированно).
У нас 13 нулей, — сдвиг вправо на 13 позиций!
| х | х | х | n | n | n | n | n | n | n | n | n | n | n | n | n |
| х | х | х |
Это результат операции И
| х | х | х |
| х | х | х |
Записывается это так: (N and 0xE000) shr 13
Можем сначала сделать сдвиг на 13 позиций а затем операцию «И» с маской, где будут все«1».
(N shr 13) and 0xFFFF
Ну вот и вся работа. Решить ее занимает времени – минут 15-20, а написать вам это все, «разжевать и в рот положить» заняло у меня 2 часа! Прекращайте, парни, начинайте уже трудиться. В учебниках все есть.
Экономика как подсистема общества: Может ли общество развиваться без экономики? Как побороть бедность и добиться.
Тема 5. Подряд. Возмездное оказание услуг: К адвокату на консультацию явилась Минеева и пояснила, что.
Отчет по производственной практике по экономической безопасности: К основным функциональным целям на предприятии ООО «ХХХХ» относятся.
Основные этапы развития астрономии. Гипотеза Лапласа: С точки зрения гипотезы Лапласа, это совершенно непонятно.
Урок 31 — 35
Арифметические и логические (битовые) операции. Маски. Арифметические и логические (битовые) операции. Маски
§26. Особенности представления чисел в компьютере. §27. Хранение в памяти целых чисел. § 28. Операции с целыми числами. §29. Хранение в памяти вещественных чисел
В главе 3, изучая основы математической логики, мы увидели, что обработка истинности и ложности высказываний может быть представлена как набор операций с двоичными кодами. Оказывается, что логические операции, введённые первоначально для обработки логических данных, можно формально применить к битам двоичного числа, и такой подход широко используется в современных компьютерах.
Рассмотрим электронное устройство для управления гирляндой лампочек. Состояние каждой лампочки будет задаваться отдельным битом в некотором управляющем регистре: если бит равен нулю, лампочка выключена, если единице — включена. Для получения различных световых эффектов (типа «бегущих огней») требуется зажигать или гасить отдельные лампочки, менять их состояние на противоположное и т. д. (рис. 4.11). Точно так же биты регистров используются для управления внешними устройствами.
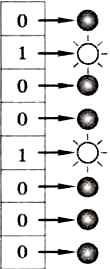
Рис. 4.11
Будем применять логические операции к каждому биту числа, как обычно, считая, что 1 соответствует значению «истина», а 0 — «ложь». Эти операции часто называют поразрядными или битовыми, поскольку действия совершаются над каждым разрядом в отдельности, независимо друг от друга 1 .
Введём несколько терминов, которые используются в литературе по вычислительной технике. Сброс — это запись в бит нулевого значения, а установка — запись единицы. Таким образом, если бит в результате какой-то операции становится равным нулю, то говорят, что он сбрасывается. Аналогично, когда в него записана единица, говорят, что бит установлен.

Маска — это константа (постоянная), которая определяет область применения логической операции к битам многоразрядного числа. С помощью маски можно скрывать (защищать) или открывать для выполнения операции отдельные биты 2 .
1 Для сравнения, сложение (как и другие арифметические действия) не является поразрядной операцией, поскольку возможен перенос из младшего разряда в старший.
2 Использование маски аналогично выделению области рисунка в графическом редакторе — для выделенных пикселей маска равна 1, для остальных — нулю.
Основные логические операции в современных процессорах — это «НЕ» (not), «И» (and), «ИЛИ» (or) и «исключающее ИЛИ» (хог).

Логическое «НЕ» (инвертирование, инверсия, not) — это замена всех битов числа на обратные значения: 0 на 1, а 1 — на 0. Эта операция используется, например, для получения дополнительного кода отрицательных чисел (см. алгоритм А1 в § 27). «НЕ» — это унарная операция, т. е. она действует на все биты одного числа. Маска здесь не используется.

Логическое «И» (and). Обозначим через D содержимое некоторого бита данных, а через М — значение соответствующего ему бита маски. Операция «И» между ними задаётся таблицей, показанной на рис. 4.12.
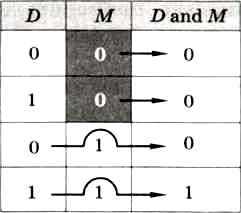
Рис. 4.12
Из таблицы видно, что при выполнении логического «И» нулевой бит в маске всегда сбрасывает (делает равным нулю) соответствующий бит результата, а единичный бит позволяет сохранить значение D (как бы пропускает его, открывая «окошко»).
С помощью логической операции «И» можно сбросить отдельные биты числа (те, для которых маска нулевая), не меняя значения остальных битов (для которых в маске стоят единицы).
Например, операция X and 1 сбросит у любого числа X все биты, кроме самого младшего. С помощью этого приёма легко узнать, является ли число чётным: остаток от деления на 2 равен последнему биту!

Логическое «ИЛИ». Вспомнив таблицу истинности логической операции «ИЛИ» (or), можно обнаружить, что в ноль в маске сохраняет бит (X or 0 = X), а единица устанавливает соответствующий бит результата (X or 1 = 1) (рис. 4.13).
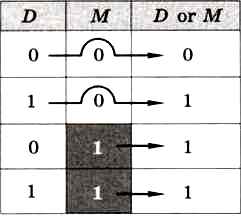
Рис. 4.13
С помощью логической операции «ИЛИ» можно установить отдельные биты числа (те, для которых маска единичная), не меняя значения остальных битов (для которых в маске стоят нули).
Например, операция X or 8016 установит старший бит восьмиразрядного числа X, формально сделав тем самым число отрицательным.
Таким образом, используя операции «И» и «ИЛИ», можно сбрасывать и устанавливать любые биты числа, т. е. строить любой нужный двоичный код. Где это может пригодиться? Рассмотрим примеры решения конкретных задач.

Пример 1. На клавиатуре набраны 3 цифры, образующие значение целого числа без знака. Определить, какое число было введено.
При нажатии клавиши на клавиатуре в компьютер поступает код нажатой клавиши. Выпишем десятичные и шестнадцатеричные коды всех символов, обозначающих цифры:

Будем пользоваться шестнадцатеричными кодами: как видно из таблицы, их связь с цифрами числа гораздо нагляднее. Чтобы получить числовое значение цифры из кода символа X, достаточно сбросить его старшие четыре бита, не изменяя значений четырёх младших битов. Для этого нужно использовать операцию X and 0F16.
Пусть S1 — код первого введённого символа, S2 — второго, S3 — третьего, а N обозначает искомое число. Тогда алгоритм перевода кодов символов в число выглядит так:
2. W = S1 and 0F16 (выделяем первую цифру).
3. N = 10 • N + W (добавляем её к числу).
4. W = S 2 and 0F16 (выделяем вторую цифру).
5. N = 10 • N + W (добавляем её к числу).
6. W = S3 and 0F16 (выделяем третью цифру).
7. N = 10 • N + W (добавляем её к числу).
Пусть, например, набраны символы ‘1’, ‘2’ и ‘3’. Тогда по таблице находим, что S1 =3116, S2 = 3216 и S3 =3316. Значение W на втором шаге вычисляется так:

Так как W = 1, на третьем шаге получаем N = 1. Следующая пара шагов — четвёртый и пятый — дают результаты W = 2 и N = 12 соответственно. Наконец, результат завершающих шагов: W = 3 и N = 123.
Такая процедура используется в каждом компьютере: именно так коды цифровых символов, набранные на клавиатуре, преобразуются в числа, с которыми компьютер выполняет арифметические действия. Заметим, что фактически здесь использована схема Горнера для представления целого числа (см. § 10).

Пример 2. Создадим структуру данных S, которая отражает, есть или нет в некотором числе каждая из цифр от 0 до 9. В математике такая структура называется множеством.
Для хранения S будем использовать 16-разрядное целое число (рис. 4.14).

Рис. 4.14
Договоримся, что младший бит числа имеет номер 0 и хранит информацию о том, есть во множестве цифра 0 (если этот бит равен 0, такой цифры нет, если равен 1, то есть). Аналогично первый бит (второй по счёту справа) показывает, есть ли во множестве цифра 1, и т. д. Старшие биты 10-15 при этом не используются. Например, во множестве, изображенном на рис. 4.14, есть только цифры 0, 3, 6 и 9.
Для записи элементов во множество и проверки их наличия удобно использовать логические операции. Рассмотрим для примера бит 5. Маска, которая потребуется для обращения к нему, — это единица в пятом разряде и нули во всех остальных, т. е. М = 002016. С её помощью можно добавить элемент к множеству с помощью операции «ИЛИ»: S = S or М. А узнать, есть ли во множестве интересующая нас цифра, можно, выделив соответствующий бит с помощью логического «И» (Р = S and М) и проверив результат на равенство нулю.

Исключающее ИЛИ. Как видно из таблицы истинности, операция «исключающее ИЛИ» (хог) не изменяет биты, когда маска нулевая, и меняет биты на противоположные при единичной маске (рис. 4.15).
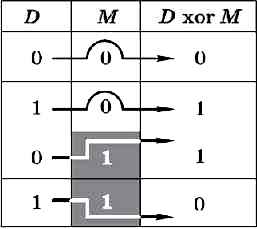
Рис. 4.15
Например, команда Y = Y хоr FF16 выполняет инверсию всех битов 8-разрядного целого числа. Напомним, что это один из этапов получения дополнительного кода отрицательных чисел.
С помощью логической операции «исключающее ИЛИ» можно выполнить инверсию отдельных битов числа (тех, для которых маска единичная), не меняя значения остальных битов (для которых в маске стоят нули).

Пример 3. Пусть X — это результат выполнения некоторого вычислительного теста, а Y — то, что ожидалось получить («правильное» значение). Нужно определить, в каких разрядах различаются эти числа (для инженера это очень полезная подсказка, где искать неисправность).
Предположим, что Х = 7, Y = 3. В результате операции X хоr У устанавливаются (в единицу) только те разряды, которые в этих числах не совпали, а остальные сбрасываются 3 . В данном случае находим, что числа различаются только одним битом:
3 Профессиональные программисты часто используют операцию хоr для обнуления переменной: команда R := R хоr R запишет в переменную R ноль, независимо от её начального значения.


Пример 4. Используя логическую операцию «исключающее ИЛИ», можно шифровать любые данные. Покажем это на примере простого текста ‘2*2=4’.
Выберем любую маску, например 2310 = 0001 01112. Эта маска представляет собой ключ шифра — зная ключ, можно расшифровать сообщение. Возьмём первый символ — цифру ‘2’, которая имеет код 5010 = ООН 00102, и применим операцию «исключающее ИЛИ» с выбранной маской:

Полученное значение 0010 01012 = 3710 — это код символа ‘%’. Для расшифровки применим к этому коду «исключающее ИЛИ» с той же маской:

В результате получили число 50 — код исходной цифры ‘2’.
Повторное применение операции «исключающее ИЛИ» с той же маской восстанавливает исходное значение, т. е. эта логическая операция обратима.
Если применить такую процедуру шифрования ко всем символам текста ‘2*2=4’, то получится зашифрованный текст ‘%=%*#’.
Обратимость операции «исключающее ИЛИ» часто используется в компьютерной графике для временного наложения одного изображения на другое. Это может потребоваться, например, для выделения области с помощью инвертирования её цвета.

Следующая страница Сдвиги

Cкачать материалы урока
Подсчет действий на калькуляторе
Изначальльное значение на калькуляторе: 1.
Определите наименьшее количество действий, необходимое, чтобы из начального числа 1 получить заданное число N.
Формат ввода
Одно целое число N.
Формат вывода
Одно целое число — минимальное количество действий, которое необходимо выполнить на данном калькуляторе.
Отображение действий в калькуляторе
калькулятор выполнял более 1 действия за раз и отброжал, так как в данном варианте он выполняет.
Последовательное выполнение арифметических действий в калькуляторе
Мне нужно сделать так, то бы калькулятор выполнял последовательные действия, то есть, если нажимать.

В калькуляторе сделать так, чтобы 4 последних результата любых действий сохранялись и выводились на экран
В калькуляторе нужно сделать так, чтобы 4 последних результата любых действий сохранялись и.

Подсчет процентов на калькуляторе
Здравствуйте. Помогите пожалуйста реализовать в калькуляторе правильный подсчет %. Должно считать.
Кабинет Информатики
Для перехода к следующему заданию все карточки должны быть перевернуты.
Задание 2. Языки и науки.

Криптография — Методы создания паролей и шифров, обеспечение конфиденциальности
Фармацевтика — Производство лекарственных средств и лекарственных веществ и проведение клинических испытаний
Компьютерное моделирование — Создание модели на компьютере приближенной к реальному объекту, например, создание модели автомобиля для проведения экспериментов
Машинное обучение — Создание моделей и алгоритмов, направленных на улучшения способностей компьютера
Симуляция процессов — Воспроизведение на компьютере процесса, который сложно показать в реальном мире. Например, прогнозирование погоды
Криптография, фармацевтика, машинное обучение и компьютерное моделирование сейчас являются наиболее развивающимися областями науки.
Задание 3. Задачи для квантового компьютера.
- Работа с паролями и шифрами
- Симуляция процессов
- Создание новых соединений молекул для производства лекарств
- Моделирование клиентского поведения
Задание 4. Будущее рядом.
Уже используют квантовые технологии:
- флешки;
- оптоволоконная связь;
- персональные компьютеры.
Будут использовать квантовые технологии:
- Логистика доставки продуктов;
- Приватность информации в месенджерах;
- Улучшение системы рекомендации видео в социальных сетях.
Задание 5. Принципы работы квантового компьютера.

Верные ответы:
1. Квантовый компьютер в качестве носителей информации использует квантовые объекты, для проведения вычислений они должны быть соединены в квантовую систему.
2. Для операций над кубитами используется система операций, называемая квантовыми вентилями.
3. Существуют универсальные наборы вентилей, с помощью которых можно выполнить любое квантовое вычисление.
4. Для получения результата работы квантового компьютера надо многократно запустить квантовый алгоритм на одном и том же входном наборе данных и усреднить результат.












