Нейронные сети: как работают и где используются
Нейронные сети часто воспринимаются как некая инновационная технология, часть мира будущего. Однако разработки в этой области начались более полувека назад, хотя прорыв произошел относительно недавно. Для людей, далеких от программирования, работа нейронной сети сродни чуду, а ее возможности кажутся безграничными.
Однако, несмотря на действительно выдающиеся возможности в некоторых областях, нейронные сети имеют свои особенности и ограничения. В нашей статье мы расскажем, как работает такой инструмент, для каких задач он подходит лучше всего и в каких сферах будет востребован в ближайшее время.
Jetson Nano

Jetson Nano — мини-компьютер стоимостью 99 долларов, предназначенный для разработчиков, интересующихся самодельной робототехникой. Несмотря на низкую цену, он оснащён сверхпроизводительной начинкой — 128-ядерным GPU-чипом Maxwell и процессором с четырьмя 64-битными ядрами ARM Cortex-A57 с суммарной производительностью 472 гигафлопс. Компьютер оснащён оптическими сенсорами с высоким разрешением и поддержкой подключения к нейронным сетям, обладает 4 ГБ оперативной памяти и несколькими портами для подключения внешней периферии вроде камер.
Jetson Nano работает на Linux и может использоваться для создания не только роботов, и, но и других умных устройств — например, смарт-колонок или хабов для управления интернетом вещей голосовыми командами. Во время работы он потребляет не более 5 ватт, так что его можно питать даже от аккумулятора.
1.2. Нейронная сеть
Нейрон (нервная клетка) является особой биологической клеткой, которая обрабатывает информацию (рис. 1). Она состоит из тела клетки (cell body), или сомы (soma), и двух типов внешних древоподобных ветвей: аксона (axon) и дендритов (dendrites). Тело клетки включает ядро (nucleus), которое содержит информацию о наследственных свойствах, и плазму, обладающую молекулярными средствами для производства необходимых нейрону материалов. Нейрон получает сигналы (импульсы) от других нейронов через дендриты (приемники) и передает сигналы, сгенерированные телом клетки, вдоль аксона (передатчик), который в конце разветвляется на волокна (strands). На окончаниях этих волокон находятся синапсы (synapses).
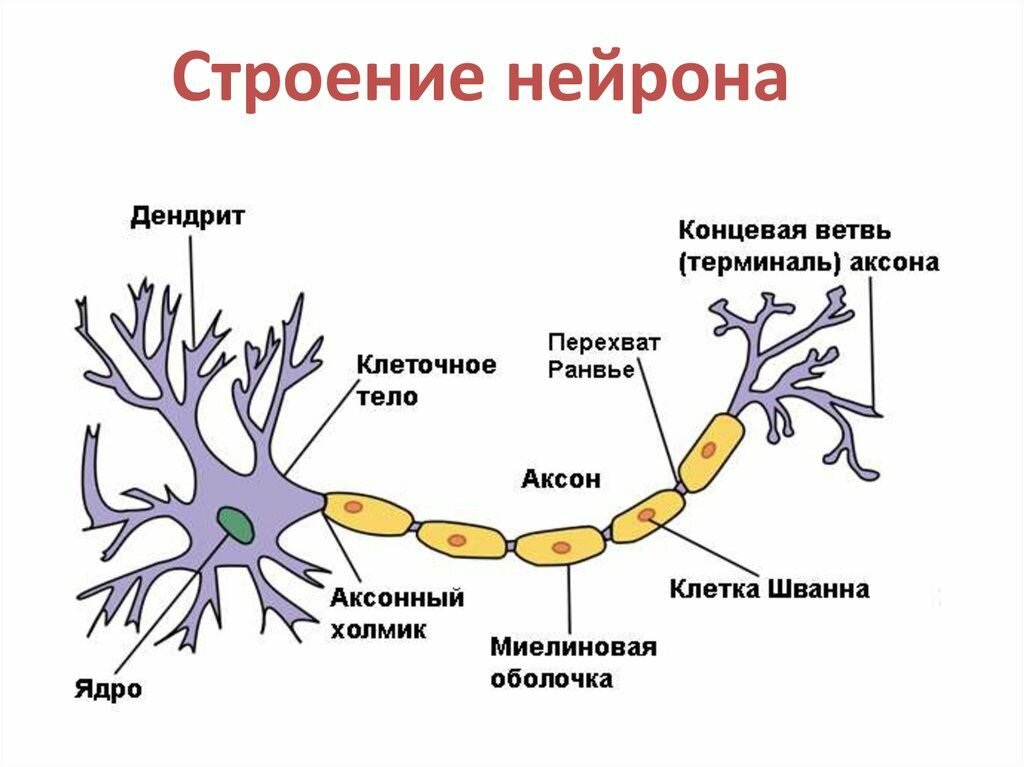
Синапс является элементарной структурой и функциональным узлом между двумя нейронами (волокно аксона одного нейрона и дендрит другого). Когда импульс достигает синаптического окончания, высвобождаются определенные химические вещества, называемые нейротрансмиттерами. Нейротрансмиттеры диффундируют через синаптическую щель, возбуждая или затормаживая, в зависимости от типа синапса, способность нейрона-приемника генерировать электрические импульсы. Результативность синапса может настраиваться проходящими через него сигналами, так что синапсы могут обучаться в зависимости от активности процессов, в которых они участвуют. Эта зависимость от предыстории действует как память, которая, возможно, ответственна за память человека.
Искусственный нейрон является структурной единицей искусственной нейронной сети и представляет собой аналог биологического нейрона.
С математической точки зрения искусственный нейрон — это сумматор всех входящих сигналов, применяющий к полученной взвешенной сумме некоторую простую, в общем случае, нелинейную функцию, непрерывную на всей области определения. Обычно, данная функция монотонно возрастает. Полученный результат посылается на единственный выход.
Искусственные нейроны (в дальнейшем нейроны) объединяются между собой определенным образом, образуя искусственную нейронную сеть. Каждый нейрон характеризуется своим текущим состоянием по аналогии с нервными клетками головного мозга, которые могут быть возбуждены или заторможены. Он обладает группой синапсов – однонаправленных входных связей, соединенных с выходами других нейронов, а также имеет аксон – выходную связь данного нейрона, с которой сигнал поступает на синапсы следующих нейронов.
Нейро́нная сеть (также искусственная нейронная сеть, ИНС) — математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма.
Говоря простым языком, нейронные сети – это сложные математические модели, принцип работы которых максимально приближен к принципу работы нервных клеток у животных.
Нейрон – это элемент нейросети, который можно визуализировать как коробочку с несколькими входными и одним выходным отверстием. Синапсы(сигналы) имеют свой вес, преобладание которого формирует исходящий из нейрона сигнал. Именно сеть таких синапсов и формирует нейросетевой комплекс.
Нейросети используются, например, в машинном обучении, выполняя различные прикладные задачи. В данном случае нейросеть используется как способ распознавания образов.
Применение нейросетей в математике позволяет решать сложные задачи с многими входными параметрами. Они также используются и в робототехнике, реализуя некоторые системы адаптивного управления устройством.
Одна из главных областей использования – искусственный интеллект. Здесь нейросеть является главным элементом в моделировании ИИ при помощи различных вычислительных формул.
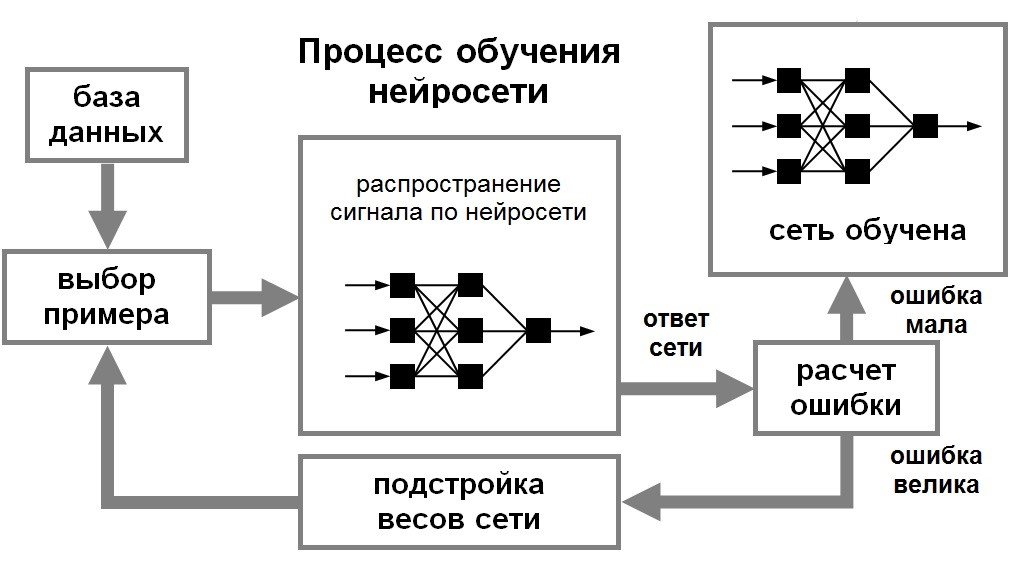
Теперь самое чумовое в нейронной сети-это способность обучаться.
Одним из главных преимуществ нейросети над другими алгоритмами, является способность последовательного обучения нейросети. Если говорить простым языком, процесс обучения подразумевает собой нахождение новых связей между нейронами, а также нахождение зависимостей между элементами цепи.
Нейронный процессор (англ. Neural Processing Unit, NPU или ИИ-ускоритель англ. AI accelerator) — это специализированный класс микропроцессоров и сопроцессоров (часто являющихся специализированной интегральной схемой), используемый для аппаратного ускорения работы алгоритмов искусственных нейронных сетей, компьютерного зрения, распознавания по голосу, машинного обучения и других методов искусственного интеллекта.
Нейронные процессоры относятся к вычислительной технике и используются для аппаратного ускорения эмуляции работы нейронных сетей и цифровой обработки сигналов в режиме реального времени. Как правило, нейропроцессор содержит регистры, блоки памяти магазинного типа, коммутатор и вычислительное устройство, содержащее матрицу умножения, дешифраторы, триггеры и мультиплексоры.
Пример использования экосистемы X-CUBE-AI
В данном разделе рассмотрен практический пример проектирования нейронной сети на базе отладочной платы NUCLEO-G474RE.
Внешний вид платы показан на рисунке 7.

Рис. 7. Внешний вид платы NUCLEO-G474RE
Эта плата содержит микроконтроллер STM32G474RET6 в корпусе с 64 выводами. Максимальная частота ядра процессора – 170 МГц, объем Flash-памяти – 512 кбайт, объем статической памяти – 128 кбайт. Также плата содержит встроенный высокоскоростной отладчик/программатор ST-LINK/V3, что позволяет производить программирование и отладку платы без использования каких-либо внешних отладочных средств.
Микроконтроллеры семейства STM32G4 обладают высокой производительностью и богатым набором периферийных устройств. Также производитель предлагает широкий набор программных и отладочных средств для разработки, в том числе решений в области нейронных сетей, поэтому представитель именно этого семейства был выбран для практического рассмотрения.
Как было показано выше, для развертывания нейросети в микроконтроллере STM32 нужна готовая тренированная модель сети. Для данного примера будет использована нейросеть HAR-CNN-Keras, исходный код которой доступен для скачивания по ссылке: Это – сверточная нейросеть, написанная с использованием открытой нейросетевой библиотеки Keras. Сеть служит для распознавания нескольких элементов активности человека, таких как спуск по лестнице, пробежка, сидение, стояние, подъем по лестнице, пешая прогулка. Входными данными для сети являются показания нескольких акселерометров, расположенных в смартфоне и обеспечивающих 20 выборок данных в секунду.
Для загрузки модели нейросети переходим по ссылке, указанной выше, и в окне проекта кликаем мышкой на файл model.h5, как это показано на рисунке 8.

Рис. 8. Выбор модели нейросети
Далее нажимаем кнопку “Download” и сохраняем файл в удобном для работы месте (рисунок 9). Для целей этого примера файл модели переименован в «har_github.h5».

Рис. 9. Загрузка файла модели
Для программирования отладочной платы необходимо установить программное обеспечение. Для начала нужно установить STM32CubeMX версии 5.1.0 или новее. На момент написания статьи самой свежей является версия программы 6.0.0. STM32CubeMX доступен как для операционной системы Windows, так и для Linux. Заодно можно скачать пакет расширения X-CUBE-AI и среду STM32CubeIDE, которая будет необходима для компиляции сгенерированного кода.
После установки STM32CubeMX пакет X-CUBE-AI устанавливается следующим образом.
- Запускается STM32CubeMX. В меню выбирается пункт «Help» → «Manage embedded software packages», можно также напрямую нажать кнопку «INSTALL/REMOVE», как это показано на рисунке 10.

Рис. 10. Выбор встроенных пакетов в STM32CubeMX
- В окне «Embedded Software Packages Manager» нажимаем кнопку «Refresh» для получения обновленного списка дополнительных модулей. Для поиска X-CUBE-AI выбираем вкладку «STMicroelectronics», как это показано на рисунке 11.

Рис. 11. Установка X-CUBE-AI в STM32CubeMX
Если X-CUBE-AI уже был установлен, желательно удалить его перед новой установкой.
- Необходимая версия пакета выбирается и устанавливается путем нажатия кнопки «Install Now». После завершения установки квадрат рядом с необходимой версией пакета становится зеленым, после чего можно нажать кнопку «Close» (рисунок 12).

Рис. 12. X-CUBE-AI в STM32CubeMX
После установки и запуска приложения STM32CubeMX выбираем пункт «ACCESS TO BOARD SELECTOR» (рисунок 13).

Рис. 13. Выбор отладочной платы NUCLEO-G474RE в STM32CubeMX
В открывшемся окне в поле «Commercial Part Number» набираем «NUCLEO-G474RE», в списке «Board List» выделяем необходимую отладочную плату (рисунок 14).

Рис. 14. Инициализация проекта
Двойным кликом запускаем проект (рисунок 15). При запуске проекта появляется сообщение “Initialize all peripherals with their Default Mode?”(«Инициализировать всю периферию в состояние по умолчанию?»). Отвечаем “Yes” («Да»).

Рис. 15. Запуск проекта
Выводы контроллера также автоматически сконфигурированы согласно трассировке отладочной платы NUCLEO-G474RE.
Тактовую частоту проекта можно проверить и, при необходимости, изменить во вкладке “Clock configuration” («Настройка тактовой частоты»), как это показано на рисунке 16.

Рис. 16. Настройка тактовой частоты
Для отладочной платы NUCLEO-G474RE максимальная частота ядра – 170 МГц. Именно это значение (параметр «HCLK (MHz)») и было выбрано (рисунок 16).
Для обмена данными с компьютером используется порт LPUART1, основные настройки которого можно посмотреть, выбрав «Categories» à «Connectivity» à «LPUART1», как это показано на рисунке 17.

Рис. 17. Настройки порта UART
Далее необходимо подключить к проекту модуль X-CUBE-AI. Для этого выбираем в меню «Software Packs» → «Select components.» Затем в открывшемся окне выбираем «STMicroelectronics.X-CUBE-AI» → «Artificial Intelligence X-CUBE-AI» → «Core», и «Application» → «Application template», как это показано на рисунке 18.

Рис. 18. Выбор модуля X-CUBE-AI
Существует несколько типов приложений, которые можно выбрать:
- System performance – для проверки производительности реализаций различных нейросетей на целевой платформе;
- Validation – для проверки производительности нейросетей и сравнения результатов вычислений;
- Application template – шаблон, позволяющий создавать пользовательские приложения. Этот тип приложения используется в данном примере и также позволяет оценить производительность и сравнить результаты вычислений.
Далее выбираем «Categories» → «STMicroelectronics.X-CUBE-AI». В окне «Configuration» → Model inputs» выбираем название для модели нейросети – в данном примере это network (рисунок 19). Тип сети – «Keras», выбираем «Saved model», то есть используется заранее сохраненная сеть. Указываем путь до файла нейросети *.h5, который был ранее загружен. Выбираем степень сжатия модели – в данном случае 8, и нажимаем кнопку «Analyze». После окончания анализа проверяем вычислительные ресурсы, необходимые для реализации данной сети с заданной степенью сжатия. Согласно рисунку 19, необходимо 367 кбайт Flash-памяти и 25 кбайт памяти RAM. В скобках рядом указаны размеры памяти выбранного микроконтроллера.

Рис. 19. Расчет вычислительных ресурсов
Коэффициент сжатия 8 был выбран из-за ограниченного объема памяти, так как модель с коэффициентом 4 уже не вместилась бы во Flash-память выбранного микроконтроллера.
Далее необходимо проверить, насколько точно код, сгенерированный для микроконтроллера, соответствует оригинальной модели нейросети. Для этого существует два вида тестов: на компьютере и на устройстве STM32 (рисунок 20).

Рис. 20. Виды проверки нейросети
Модель нейросети, сгенерированная на языке С, запускается на выполнение на процессоре х86 или STM32, и результат выполнения сравнивается с оригинальной моделью. При ошибке L2 меньше 0,01 результат построения С-модели считается успешным. Большое влияние на ошибку оказывает степень сжатия.
Сначала проверяется модель на компьютере в среде х86. После нажатия кнопки «Validate on desktop» открывается окно, отображающее процесс проверки. В данном случае в качестве входных данных используются случайные числа. Результат выполнения проверки на компьютере показан на рисунке 21.

Рис. 21. Результат проверки модели на компьютере
Ошибка L2 = 5,01e-07, что значительно меньше допустимой погрешности 0,01. Также виден процент использования вычислительных ресурсов разными слоями нейросети.
Для проверки модели на STM32 нажимаем кнопку «Validate on target». При этом открывается окно конфигурации проверки (рисунок 22).

Рис. 22. Настройка проверки модели в STM32
Имя порта зависит от операционной системы. В данном примере использовалась система Ubuntu18.04, где порт для связи с отладочной платой получил автоматическое название /dev/ttyACM0. В операционной системе Windows это будут названия типа COM1, COM2 и так далее. Скорость 115200 соответствует настройкам проекта. Для проверки модели в микроконтроллере необходима среда (Toolchain/IDE) для компиляции исходных кодов, сгенерированных с помощью STM32CubeMX. В данном случае для компиляции используется среда STM32CubeIDE, которая была предварительно установлена на компьютер.
После выполнения необходимых настроек нажимаем «OK» и ожидаем выполнения теста, который включает в себя компиляцию проекта, прошивку платы, выполнение теста, анализ полученных результатов. На рисунке 23 показан результат выполнения теста.

Рис. 23. Результат выполнения теста в STM32
Ошибка L2 в этом случае также значительно меньше 0,01, а значит модель, сгенерированная для микроконтроллера STM32, соответствует оригинальной.
Устанавливаем tensorflow
Tensorflow — открытая библиотека для машинного обучения и работы с нейросетями. Она будет отвечать за то, чтобы наш компьютер мог запустить нейросеть и правильно с ней работать.
Для установки пишем команду:
pip install tensorflow
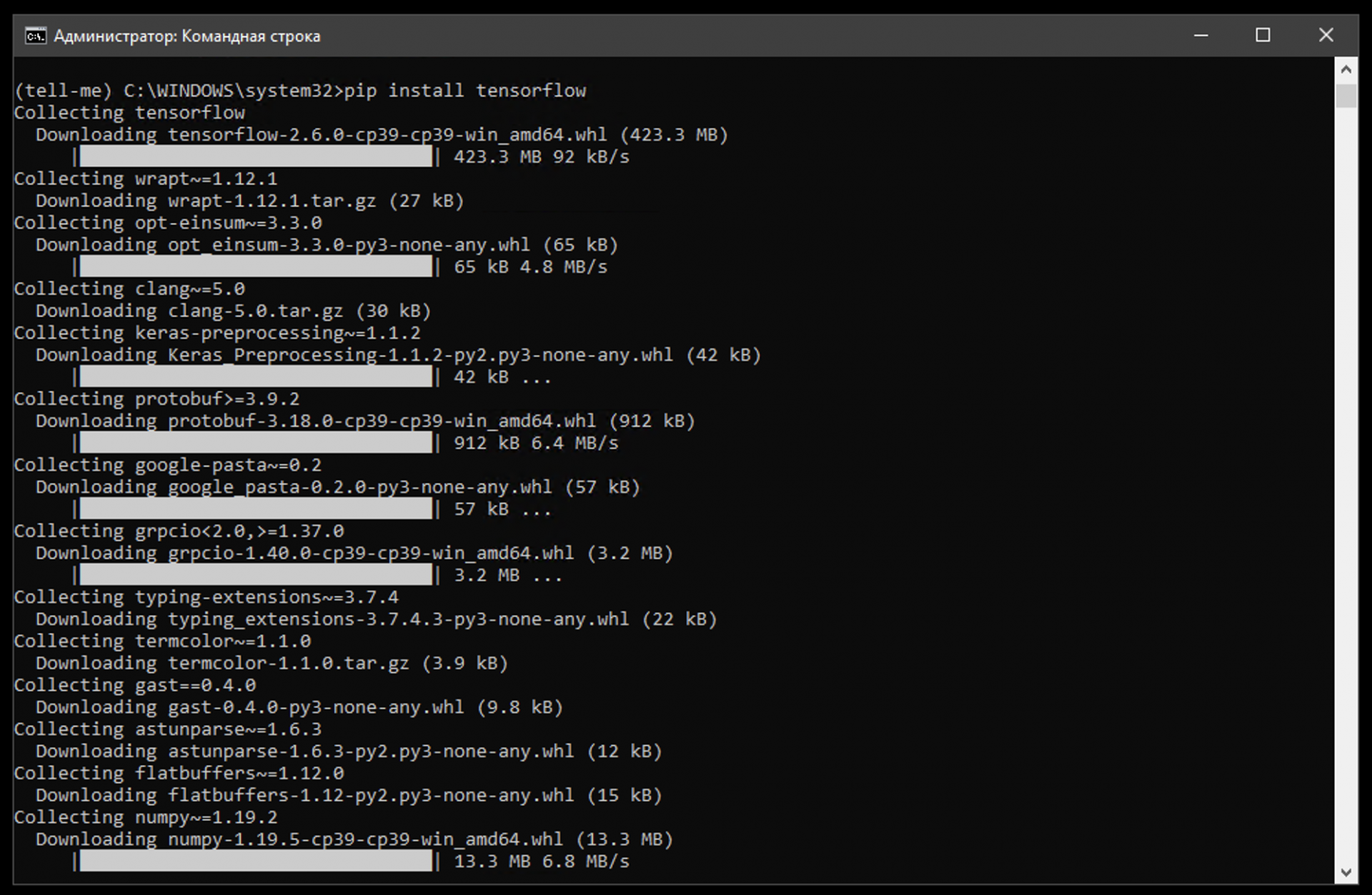
pip — это программа, которая отвечает в Python за скачивание, установку и обновление библиотек и вспомогательных пакетов. Это как магазин приложений Apple, только для командной строки и для разработчиков.
Чтобы убедиться, что библиотека установилась правильно и работает штатно, проверим её простым тестом.
1. Пишем команду:
2. Начало командной строки поменялось на >>> — это значит, питон готов к приёму своих команд. Пишем по очереди такое:
hello = tf.constant(‘Hello, TensorFlow’)
sess = tf.compat.v1.Session()
print(sess.run(hello))
Если в ответ питон нам выдал что-то вроде ‘Hello, TensorFlow’, это значит, что мы всё сделали правильно.

Нейронные сети
скусственные нейронные сети, подобно биологическим, являются вычислительной системой с огромным числом параллельно функционирующих простых процессоров с множеством связей. Несмотря на то что при построении таких сетей обычно делается ряд допущений и значительных упрощений, отличающих их от биологических аналогов, искусственные нейронные сети демонстрируют удивительное число свойств, присущих мозгу, это обучение на основе опыта, обобщение, извлечение существенных данных из избыточной информации.
Нейронные сети могут менять свое поведение в зависимости от состояния окружающей их среды. После анализа входных сигналов (возможно, вместе с требуемыми выходными сигналами) они самонастраиваются и обучаются, чтобы обеспечить правильную реакцию. Обученная сеть может быть устойчивой к некоторым отклонениям входных данных, что позволяет ей правильно «видеть» образ, содержащий различные помехи и искажения.
В 50-х годах прошлого века группа исследователей объединила биологические и физиологические подходы и создала первые искусственные нейронные сети. Тогда казалось, что ключ к искусственному интеллекту найден. Но, хотя эти сети эффективно решали некоторые задачи из области искусственного зрения предсказания погоды и анализа данных, иллюзии вскоре рассеялись. Сети были не в состоянии решать другие задачи, внешне похожие на те, с которыми они успешно справлялись. С этого времени начался период интенсивного анализа. Были построены теории, доказан ряд теорем. Но уже тогда стало понятно, что без привлечения серьезной математики рассчитывать на значительные успехи не следует.
С 70-х годов в научных журналах стали появляться публикации, касающиеся искусственных нейронных сетей. Постепенно был сформирован хороший теоретический фундамент, на основе которого сегодня создается большинство сетей. В последние два десятилетия разработанная теория стала активно применяться для решения прикладных задач. Появились и фирмы, занимающиеся разработкой прикладного программного обеспечения для конструирования искусственных нейронных сетей. К тому же 90-е годы ознаменовались приходом искусственных нейронных сетей в бизнес, где они показали свою реальную эффективность при решении многих задач от предсказания спроса на продукцию до анализа платежеспособности клиентов банка.
Сегодня существует большое число различных конфигураций нейронных сетей с различными принципами функционирования, которые ориентированы на решение самых разных задач. В качестве примера рассмотрим многослойную полносвязанную нейронную сеть прямого распространения (рис. 1), которая широко используется для поиска закономерностей и классификации образов. Полносвязанной нейронной сетью называется многослойная структура, в которой каждый нейрон произвольного слоя связан со всеми нейронами предыдущего слоя, а в случае первого слоя со всеми входами нейронной сети. Прямое распространение сигнала означает, что такая нейронная сеть не содержит петель.
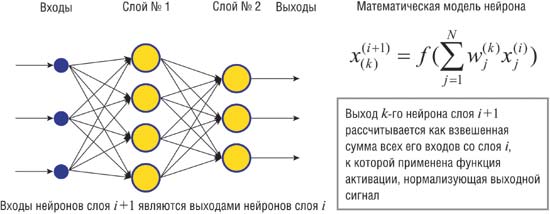
Рис. 1. Пример многослойной полносвязанной нейронной сети прямого распространения сигнала
Многослойный перцептрон
Рассмотрим функцию Y=f(X), которая ставит в соответствие m-мерному вектору X некоторый p-мерный вектор Y (Рис. 1). Например, в задаче классификации вектор X- это классифицируемый объект, характеризуемый m признаками; вектор Y, состоящий из одной единицы и остальных нулей, является индикатором класса, к которому принадлежит вектор X (позиция единицы означает номер класса). Функция f ставит в соответствие каждому объекту тот класс, к которому он принадлежит.
Предположим, нам нужно найти функцию f. Воспользуемся методом обучения на примерах. Предположим, что имеется репрезентативная выборка векторов Xi, для которых известно значение функции Yi=f(Xi). Набор пар (Xi,Yi) будем называть обучающей выборкой. Рассмотрим теперь нейронную сеть, называемую многослойным перцептроном, определив, как устроены элементы сети («нейроны»), какова архитектура связей между элементами и по каким правилам будет происходить обучение сети.
Элемент сети функционирует в дискретном времени и на основании поступивших сигналов формирует результирующий сигнал. Элемент имеет несколько входов, каждому из которых предписан определенный «вес». Сигналы, поступающие по входам, суммируются с учетом соответствующих весов, и суммарный сигнал сравнивается с порогом срабатывания. Если суммарный сигнал меньше порога, то сигнал на выходе элемента близок или равен нулю, в противном случае сигнал близок к единице.
Каждый элемент входного слоя имеет один вход (с весом 1), по которому поступает соответствующая компонента вектора X. Каждый элемент скрытого слоя получает сигналы ото всех элементов входного слоя. Тем самым, элемент скрытого слоя имеет m входов, связывающих его с элементами входного слоя. Связи от элементов входного слоя к элементам скрытого слоя характеризуются матрицей «весов» связей w1, компоненты которой определяют величину эффективности связи. Каждый элемент выходного слоя получает сигналы ото всех элементов скрытого слоя. Таким образом, подавая на входной слой сети вектор X, мы получаем вектор активности элементов скрытого слоя и затем вектор Y на элементах выходного слоя. Результат работы сети зависит от числовых значений весов связей между элементами.
Обучение сети состоит в правильном выборе весов связей между элементами. Выбираются такие веса связей, чтобы суммарная среднеквадратичная ошибка для элементов обучающей выборки была минимальной. Достичь этого можно разными методами . После обучения перцептрона проводится процедура тестирования, позволяющая оценить результаты работы. Для этого обучающую выборку обычно делят на две части. Одна часть используется для обучения, а другая, для которой известен результат, задействована в процессе тестирования. Процент правильных результатов работы сети на этапе тестирования является показателем качества работы перцептрона.
Надо сказать, что для очень многих практических задач удается достичь на удивление высокого качества работы сети (порядка 95% и выше). Существует ряд математических теорем , обосновывающих возможность применения многослойных перцептронов для аппроксимации достаточно широкого класса функций f.
Проиллюстрируем применение многослойных перцептронов на примере решения задачи сжатия информации. Такая необходимость часто возникает в различных приложениях, в частности, при распознавании образов существует этап предобработки, когда исходные данные представляются в компактной, удобной форме. Результаты этого этапа зачастую определяют успех в решении задачи распознавания.
Популярный метод сжатия информации был предложен в 1987 г. G.Cottrell, P.Munro, D.Zipser . Рассмотрим трехслойный перцептрон, у которого число элементов входного и выходного слоев одинаково, а число элементов скрытого слоя значительно меньше. Предположим, что в результате обучения на примерах (на векторах обучающей выборки) перцептрон может воспроизводить на выходе тот же самый вектор X, который подается на входной слой перцептрона. Такой перцептрон автоматически осуществляет сжатие информации: на элементах скрытого слоя возникает представление каждого вектора, которое значительно короче, чем длина вектора, подаваемого на вход. Предположим, что некоторый набор векторов нужно передавать по линии связи, предварительно сжимая информацию и тем самым уменьшая число каналов, необходимых для ее передачи. Поместим на одном конце линии входной и скрытый слои перцептрона, а результат работы элементов скрытого слоя (короткие векторы) будем передавать по линии связи. На другом конце линии поместим копию скрытого слоя и выходной слой, тогда переданный короткий вектор с элементов скрытого слоя перейдет на элементы выходного слоя, где будет воспроизведен исходный вектор (декомпрессия).












