Кодирование текстовой информации в компьютере

Системы счисления

В этом гайде разберемся, что такое системы счисления, для чего программисты используют непривычные способы для записи чисел и как их понимать.

С давних пор людям нужно было записывать числа. В торговле числа нужны, чтобы знать, сколько товаров есть на складе и сколько денег принесла сделка. Записи о положении небесных тел помогли шумерам составить первый календарь, а календарь, в свою очередь, пригодился, чтобы заранее готовиться к посевным и сбору урожая. Строительные сметы, переписи населения, распределение наследства — числа оказались очень востребованными даже в самых древних государствах.

Так что люди научились записывать числа в незапамятные времена. Небольшие числа легко записывались зарубками или насечками, но если в числе несколько знаков, требуется иная система записи. Эту проблему в разных странах решали по-разному.

Сейчас разные способы записи чисел называются системами счисления.

Систем счисления было придумано довольно много, и даже в наши дни мы используем две системы, возникшие в далёкой древности. Из Древнего Рима к нам пришла римская система счисления, где цифры обозначаются буквами латинского алфавита. За основу римляне взяли количество пальцев на одной руке — 5, и на двух руках — 10. Числа 1, 5 и 10 в римской системе обозначаются буквами I, V и X, и с помощью них можно записать любое число от 1 до 49. Например, VII это 7, а XIX — 19.

От Древних Шумеров мы научились делить дроби на шестьдесят частей. Именно из-за них в нашем часе 60 минут, а в минуте 60 секунд. Шумерская система счисления так и называется — шестидесятеричная. Но, конечно, наиболее привычной выглядит численная запись в системе, которую придумали в Древней Индии. Сейчас ее называют арабской или десятичной системой счисления.

Какие бывают символы?

В роли символов для компьютера выступают не только русские, английские и другие буквы, но и еще знаки препинания, а также другие знаки. Даже пробел, которым мы разделяем слова при печатании на компьютере, устройство воспринимает как символ. Чем-то очень напоминает высшую математику, ведь там, по мнению многих профессоров, ноль имеет двойное значение: он и является числом, и одновременно ничего не обозначает. Даже для философов вопрос пробела в тексте может стать актуальной проблемой. Шутка, конечно, но, как говорится, в каждой шутке есть доля правды.

Десятичная система

Десятичная система записи чисел, которой мы привыкли пользоваться в повседневной жизни, с которой мы знакомы с детства, в которой производим все наши вычисления, — пример позиционной системы счисления. Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Алгоритмические числа образуются в ней следующим образом: значения цифр умножаются на «веса» соответствующих разрядов, и все полученные значения складываются. Это отчётливо прослеживается в числительных русского языка, например: «три-ста пять-десят семь».

Основанием позиционной системы счисления может служить любое натуральное число q > 1. Алфавитом произвольной позиционной системы счисления с основанием q служат числа 0, 1, …, q—1, каждое из которых может быть записано с помощью одного уникального символа; младшей цифрой всегда является 0.

Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов, необходимых для записи любых чисел.

В позиционной системе счисления с основанием q любое число может быть представлено в виде:

• А — число;
• q — основание системы счисления;
• а_i — цифры, принадлежащие алфавиту данной системы счисления;
• n — количество целых разрядов числа;
• m — количество дробных разрядов числа;
• q i — «вес» i-го разряда.

Запись числа по формуле (1) называется развёрнутой формой записиСвёрнутной формой записи числа называется его представление в виде 1 ± a_n-1a_n-2…a₁a₀,a_-1…a_-m. 1 Далее будут рассматриваться только положительные целые числа.

Пример 3. Рассмотрим десятичное число 14351,1. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развёрнутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:

• 1 • 10 4 + 4 • 10 3 + 3 • 10 2 + 5 • 10 1 + 1 • 10 0 + 1 • 10 -1 .

Обработка графических изображений

Кодирование текстовой, звуковой и графической информации осуществляется в целях ее качественного обмена, редактирования и хранения. Кодировка информационных сообщений различного типа обладает своими отличительными чертами, но, в целом, она сводится к преобразованию их в двоичном виде.

Рисунки, иллюстрации в книгах, схемы, чертежи и т.п. – примеры графических сообщений. Современные люди для работы с графическими данными все чаще применяют компьютерные технологии.

Суть кодирования графической и звуковой информации заключается в преобразовании ее из аналогового вида в цифровой.

Кодирование графической информации – это процедура присвоения каждому компоненту изображения определенного кодового значения.

Способы кодирования графической информации подчиняются методам представления изображений (растрового или векторного):

1. Принцип кодирования графической информации растровым способом заключается в присвоении бинарного шифра пикселям (точкам), формирующим изображение. Код содержит сведения о цветовых оттенках каждой точки. Примером служат снимки, сделанные на цифровом фотоаппарате.

1. Векторная кодировка осуществляется благодаря использованию математических функций. Компонентам векторных изображений (точкам, прямым и другим геометрическим фигурам) присваивается двоичная последовательность, определяющая разнообразные параметры. Такая графика зачастую применяется в типографии.

Источник

Многим станет интересно: «В чем суть кодирования графической информации, представленной в виде 3D-изображений?» Дело в том, что работа с трехмерными данными сочетает способы растровой и векторной кодировки.

Кодирование и обработка графической информации различного формата имеет как свои преимущества, так и недостатки.

Что такое восьмеричная система счисления?

Восьмеричная система счисления не так широко используется, как шестнадцатеричная двоичная. Он был разработан по той же идее, что и шестнадцатеричная система: сделать двоичную систему более компактной.

В восьмеричной системе двоичные числа группируются в тройки вместо квартетов. Итак, восьмеричная система — это основание-8, так как2 ^ 3 = 82Взаимодействие с другими людьми3Взаимодействие с другими людьмиВзаимодействие с другими людьми= 8.

Мы используем восемь основных символов для восьмеричной системы, которые заимствованы из десятичной системы. Двоичные триплеты могут иметь значения в диапазоне от0-70 — 7.

Значения разряда будут возрастать по возрастанию 88 справа налево.

Чтобы преобразовать двоичное в восьмеричное, мы следуем этой базовой технике:

• Сгруппируйте двоичное число в наборы по три (аналогично тому, что мы сделали с шестнадцатеричным).
• Довести каждую группу цифр до числа, кратного трем, путем добавления нулей
• Напишите соответствующий восьмеричный символ под каждой группой.
• Теперь у вас будет восьмеричное число

Преобразование восьмеричного числа в двоичное аналогично, но немного проще:

• Запишите двоичное представление для каждой восьмеричной цифры
• Соедините эти числа вместе
• У вас не будет двоичного числа

Двоичное кодирование звуков

Еще одна причина, почему двоичное кодирование является универсальным методом программирования информации, — это его простота при работе с аудиофайлами. Любая музыка представляет собой звуковые волны разной амплитуды и частоты колебания. От этих параметров зависит громкость звука и его высота тона.

Чтобы запрограммировать звуковую волну, компьютер делит ее условно на несколько частей, или «выборок». Число таких выборок может быть большим, поэтому существует 65536 различных комбинаций нулей и единиц. Соответственно, современные компьютеры оснащены 16-битными звуковыми картами, что означает использование 16 двоичных цифр для кодирования одной выборки звуковой волны.

Чтобы воспроизвести аудиофайл, компьютер обрабатывает запрограммированные последовательности двоичного кода и соединяет их в одну непрерывную волну.

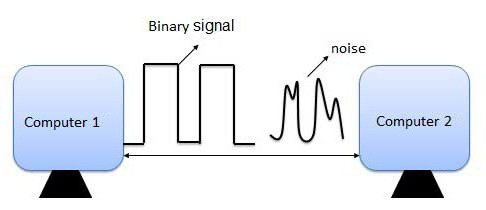
Зачем кодировать информацию?

Во-первых, необходимо ответить на вопрос для чего кодировать информацию? Дело в том, что компьютер способен обрабатывать и хранить только лишь один вид представления данных – цифровой. Поэтому любую входящую в него информацию необходимо переводить в цифровой вид.

Чтобы все компьютеры могли однозначно понимать тот или иной текст, необходимо использовать общепринятые стандарты кодирования текста. В прочих случаях потребуется дополнительное перекодирование или несовместимость данных.

ASCII

Самым первым компьютерным стандартом кодирования символов стал ASCII (полное название — American Standart Code for Information Interchange). Для кодирования любого символа в нём использовали всего 7 бит. Как вы помните, что закодировать при помощи 7 бит можно лишь 27 символов или 128 символов. Этого достаточно, чтобы закодировать заглавные и прописные буквы латинского алфавита, арабские цифры, знаки препинания, а так же определенный набор специальных символов, к примеру, знак доллара — «$». Однако, чтобы закодировать символы алфавитов других народов (в том числе и символов русского алфавита) пришлось дополнять код до 8 бит (28=256 символов). При этом, для каждого языка использовалась свой отдельная кодировка.

UNICODE

Нужно было спасать положение в плане совместимости таблиц кодировки. Поэтому, со временем были разработаны новые обновлённые стандарты. В настоящее время наиболее популярной является кодировка под названием UNICODE. В ней каждый символ кодируется с помощью 2-х байт, что соответствует 216=62536 разным кодам.

ГЛАВА 7 Оценка ERP-систем

ГЛАВА 7 Оценка ERP-систем Уровень приложений находится на промежуточном слое системы SAP, который называется Базис-система SAP R/3. Базис-система — это слой, который позволяет делать приложения мобильными, и обеспечивает их независимость от особенностей конкретной

1.8. Быстрый поиск информации с помощью Spotlight Spotlight — функция сверхбыстрого, эффективного, гибкого поиска информации. В разд. 1.4.2 были рассмотрены примеры использования функции Spotlight для поиска файлов и папок в окне Finder.Но к функции Spotlight можно обратиться в любой момент