Компьютер запрашивает радиус круга и сторону квадрата надо определить у какой фигуры площадь больше

Задание по планиметрии.

Этот раздел содержит геометрические задачи ЕГЭ по математике на следующие темы:

Задачи на формулы площади.
Задачи на площадь фигуры на клетчатой бумаге.
Задачи на площадь фигуры на координатной плоскости.

В демонстрационных вариантах ЕГЭ 2022 года они могут встретиться под номерами 5, 10, 15 для базового уровня и под номером 3 для профильного уровня.

Внимание: Для усиления обучающего эффекта ответы и решения загружаются отдельно для каждой задачи последовательным нажатием кнопок на желтом фоне. (Когда задач много, кнопки могут появиться с задержкой. Если кнопок не видно совсем, проверьте, разрешен ли в вашем браузере JavaScript.)

По диагонали и стороне

Должна быть известна диагональ и любая из сторон. Действия:

Найти квадрат диагонали, то есть умножить ее на саму себя.
Найти квадрат известной стороны.
Из квадрата диагонали вычесть квадрат стороны.
Найти квадратный корень получившейся разности.
Умножить его на известную сторону.

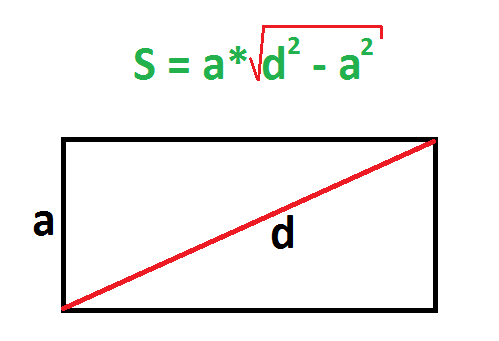
Ищем площадь по диагонали и стороне

Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.

Квадрат стороны = 3*3 = 9 см.
Квадрат диагонали = 5*5 = 25 см.
Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
Умножаю корень разности на известную сторону: 16*9 = 144 см.

Обратите внимание

Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.

Международный конкурс детско-юношеского творчества «В ЦАРСТВЕ ЛЮБИМЫХ СКАЗОК »

Если вам понравилась статья, лучший способ сказать cпасибо — это поделиться ссылкой со своими друзьями в социальных сетях 🙂

Предыдущая работа
Следующая работа

Также вас может заинтересовать

Конспект занятия по математике для 5 класса «Самостоятельная работа по теме «Решение задач на обыкновенные дроби», 5 класс математика.» Математика
Разное по математике для 6 класса «Игры-путешествия на уроках математики как средство повышения познавательной активности учащихся в рамках гражданско-патриотического воспитания.» Математика
Конспект занятия по математике для дошкольников «»Ориентировка в пространстве»» Математика
Уроки по математике для 5 класса «Разработка урока с применением электронных технологий обучения на тему: «Точка, плоскость, прямая, отрезок, луч»» Математика
Конспект занятия по математике для 1 класса «Конспект урока по математике для 1 класса. Тема: «Признаки предметов: размер, форма, цвет».» Математика

Найти площадь закрашенной области: S

Площадь искомой области можно выразить как разницу между площадью квадрата и площадью круга

Формула разницы площадей

Формула Площадь квадрата

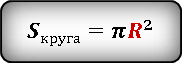
Площадь круга

Неизвестен радиус окружности. Из рисунка видно, что сторона квадрата равна диаметру окружности и соответственно удвоенному радиусу

сторона квадрата равна диаметру окружности или удвоенному радиусу

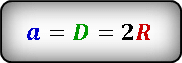
Выразим радиус окружности через сторону квадрата и подставив значение, получим радиус окружности.

находим радиус окружности

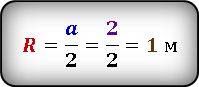
Формула площади искомой области на основании выкладок выше, будет выглядеть следующим образом.

Формула площади искомой области

Подставив уже известные значения стороны квадрата и радиуса окружности, получаем.

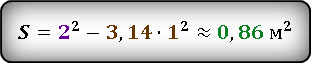
Формула разницы площадей

По стороне и периметру – 1 способ

Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).

Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.

Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.

Нахожу вторую сторону прямоугольника:
1. P=2(a+b).
2. P=2a+2b.
3. 14= 2*3+2b.
4. 14 = 6+2b.
5. 2b = 14-6 = 8.
6. b = 8/2.
7. b = 4.
Окружность описанная вокруг квадрата

Кругом описанным вокруг квадрата называется круг проходящий через четыре вершины квадрата и имеющий центр на пересечении диагоналей квадрата.

Радиус окружности описанной вокруг квадрата всегда больше радиуса вписанной окружности в√ 2 раз.

Радиус окружности описанной вокруг квадрата равен половине диагонали.

Площадь круга описанного вокруг квадрата большая площадь того же квадрата в π/2 раз.

Формулы определения радиуса окружности описанной вокруг квадрата

1. Формула радиуса окружности описанной вокруг квадрата через сторону квадрата:

R = a √ 2

2

2. Формула радиуса окружности описанной вокруг квадрата через периметр квадрата:

R = P

4√ 2

3. Формула радиуса окружности описанной вокруг квадрата через площадь квадрата:

R = √ 2S

2

4. Формула радиуса круга описанного вокруг квадрата через диагональ квадрата:

R = d

2

5. Формула радиуса круга описанного вокруг квадрата через диаметр описанной окружности:

R = D_о

2

7. Формула радиуса круга описанного вокруг квадрата через диаметр вписанной окружности:

R = D_в √ 2

2

8. формула радиуса круга описанного вокруг квадрата через длину отрезка l :

R = l √ 10

5

Формулы вычисления радиуса описанной окружности

Через сторону квадрата

Радиус R окружности, описанной около квадрата, равняется длине его стороны a, умноженной на квадратный корень из двух и деленной на два.

Через диагональ квадрата

Радиус R описанной вокруг квадрата окружности равен половине его диагонали d.

Примеры решения задач

Задача 1

Найдите площадь круга, если известен его радиус см.

Решение: Для определения площади круга используем формулу (1):

см 2 . Сейчас мы имеем точное значение площади круга. Но если мы возьмем вместо число 3,14, то получим приближенное значение площади круга:

см 2 .

Задача 2

Найдите площадь земельного участка, если известно, что форма участка — круг, а диаметр участка составляет 50 м.

Решение: Чтобы найти площадь земельного участка, мы должны рассчитать площадь круга с диаметром 50 м. Используем формулу (2):

$S=pi frac{d^2}{4}=pi frac{50^2}{4}=62,5 pi approx 62,5 cdot 3,14 approx 196,25$

м 2 .

Ответ: м 2 .

Задача 3

Длина границы земельного участка круглой формы равна 64 м. Найдите площадь участка.

Решение: граница участка круглой формы — это окружность. Тогда длина этой границы — это длина окружности. Площадь участка — площадь круга, которую мы определим по формуле (3) через длину окружности:

$S=frac{l^2}{4 pi}=frac{64^2}{4 pi}=frac{1024}{pi} approx frac{1024}{3,14} approx 326,11$

м 2 .

Ответ: м 2 .

Для того, чтобы определять площадь круга в задачах по геометрии вам нужно определить с тем, какие данные вам известны и использовать те формулы для определения площади круга, которые больше всего подходят.

И насколько это точно?

Действительно, осталось определиться с точностью данного метода. Конечно, всё зависит от количества точек, и здесь нужно соблюдать золотую середину — десяти для нашего примера было бы явно недостаточно, а от тысячи слишком рябило бы в глазах. Поэтому попробуем определить погрешность для трёхсот точек и описанного квадрата со стороной 20 см. Для этого возьмём фигуру, площадь которой нам известна заранее. Например, такую:

Проставляем точки:

Результаты заносим в таблицу:

0 6 11 8 5 0

9 15 8 5 13 2

11 8 5 14 13 5

10 11 8 8 4 4

2 14 9 10 4 1

0 3 5 6 0 0

Рассчитываем площадь фигуры:
площадь описанного прямоугольника — 20 см х 20 см = 400 кв. см;
количество точек в прямоугольнике — 300;
количество точек внутри фигуры (сумма значений из таблицы) — 237;
площадь фигуры — 316 кв. см.

Нетрудно посчитать, что реальная площадь круга с радиусом 10 см составляет 314,16 кв. см. Таким образом, погрешность метода составила 0,59%, чего в большинстве случаев достаточно для прикладного использования.