Целые и вещественные числа в памяти компьютера
Рассматриваемая тема не обязательно связана с объединением, она представляет также самостоятельный интерес. Здесь этот материал нужен для понимания некоторых примеров этого и последующих параграфов.
Вещественное число (число с плавающей запятой) состоит из двух частей: мантиссы и порядка. Например, число в десятичной системе счисления 0,000123 можно записать одним из следующих способов: 0.0000123*10; 0,123*10 -3 ; 1,23*10 -4 и т.д. Аналогично 78900=0,789*10 5 =78,9*10 3 и т.д. Термин “число с плавающей запятой” и связан с тем, что десятичная запятая перемещается (плывёт) по числу. Из такого рода различных записей в десятичной системе счисления нас будет интересовать нормализованное число, соответственно 0,123*10 -3 и 0,789*10 5 . Первая его часть называется мантиссой (0,123 и 0,789), а числа -3 и 5 – порядком.
Аналогично различные варианты записи (на бумаге, а не в памяти компьютера) вещественного числа имеют место и в двоичной системе счисления. Например, рассмотрим десятичное число 12,375. Для его перевода в двоичную систему счисления отдельно переводим целую часть (см. гл. 4 файла Lections1Semestr) и отдельно дробную часть. В качестве вспомогательной системы счисления можно использовать шестнадцатеричную. Для перевода дробной части из 10 с.с в 16 с.с выполняем следующее:
дробную часть числа умножаем на 16;
полученную целую часть результата (число от 0 до 15) переводим в 16-ю с.с и берём в качестве первой после запятой 16-й цифры результата;
дробную часть результата, если она не равна нулю, повторно умножаем на 16;
полученную целую часть переводим в 16-ю с.с и берём в качестве следующей 16-й цифры;
дробную часть результата снова умножаем на 16;
это продолжаем, пока не наступит одна из следующих ситуаций:
a) на некотором шаге, не обязательно в самом начале, получим в дробной части нуль. В этом случае перевод выполнили точно. Это имеет место в нашем примере: 0,375*16=6.0;
b) получим в дробной части число, которое было раньше. Например, 0,15*16=2,4; 0,4*16=6,4. Если продолжать умножение 0,4*16, будем получать одно и то же, т. е 6,4. В таком случае получаем следующий результат: 0,1510= 0,2666…16=0,2(6)16. Круглые скобки означают, что записанное в них одно или несколько разных чисел будут повторяться бесконечное число раз. Говорят, что это число в периоде, т.е. 6 в периоде;
c) если не получаем ни нуль, ни повторяющиеся числа, то ограничиваемся заданным предварительно количеством двоичных или шестнадцатеричных цифр. Для числа типа float необходимо получить 24 двоичные цифры, считая от первой значащей, или не менее 7 шестнадцатеричных цифр, не считая первые 16-е нули.
Для перевода дробной части из 16-й в 2-ю с.с. записываем каждую 16-ю (но не 10-ю!) цифру в виде тетрады, т.е. четырёх двоичных цифр. Получим 12.37510=С.616=1100,0110. При этом последнюю цифру ‘0’ можем не писать. Как и в 10-й с.с., этот нуль незначащий. Остальные нули рядом с десятичной запятой обязательны!
Это двоичное число, как и в 10-й с.с., записать можно по-разному: 11,00011*2 2 ; 1100011*2 -3 ; 1.100011*2 3 . Из приведенных вариантов нас будет интересовать последняя нормализованная запись, в которой в целой части записана одна первая значащая единица. Получим: m= памяти не хранится, но 1.100011; p=310=112, где m —нормализованная мантисса, p — порядок в 2 с.с.
Пусть число объявлено как float. Тогда 4 байта (32 бита) распределяются следующим образом:
один самый “левый” бит отводится под знак мантиссы, или, что то же самое, под знак всего числа. Записывается 0, если мантисса, а, значит и само вещественное число, положительное, и 1 в противном случае. Никакого дополнительного кода для отрицательного вещественного числа, как это было для целых чисел, получать не надо;
следующие 8 разрядов (бит) занимает изменённый порядок записи числа в 2-й с.с., который называется характеристикой числа. Обозначим её x. Знак порядка нигде не хранится. Чтобы он всегда был неотрицательным, порядок увеличивается на 12710, т. е. x=p+12710=p+7F16. (1)
Для нашего примера здесь будет храниться число x=310+12710= 13010=8216=100000102. Это же можно вычислить и так: x=316+7F16=8216 =100000102 ;
последние 23 (32-1-8) разряда занимает мантисса. При этом целая её часть, равная 1, в памяти не хранится, но учитывается при вычислениях. Если дробная часть числа переведена в 16-ю, а, значит и в двоичную с.с не точно, т. е. имели место варианты b) и c) (см. выше перевод), последняя 2-я цифра округляется по обычным правилам. Если первая отбрасываемая 2-я цифра равна 1, то прибавляем двоичную единицу, в противном случае оставляем без изменения.
Таким образом, число 12,375 в формате float будет представлено следующим образом: 01000001010001100000000000000000. Иногда в литературе можно встретить шестнадцатеричную запись этого результата: 4146000016.
Упражнение. Представить число -0.01 как число с плавающей точкой в формате float.
Переводим модуль числа в шестнадцатеричную, а затем в двоичную системы счисления описанным выше способом:
Так как под мантиссу отводится 23 разряда, то должны получить 25 двоичных цифр, не считая первых после десятичной точки подряд идущих нулей. Почему? По правилу нормализации самая первая значащая единица (в примере в десятичной цифре 2) в память не записывается, а ещё одна дополнительная двоичная цифра нужна для того, чтобы определить, как округлять число. Так как первая отбрасываемая двоичная цифра =0, то получаем
Если число “маленькое”, т.е. целая часть =0, а в дробной части после запятой несколько подряд идущих нулей, то получим отрицательный порядок. Так как 0.0000001010001111010111000010102 = 1.01000111101011100001010*2 -7 ,
В результате получим ответ: 10111100001000111101011100001010.
Рассмотрим обратную задачу. Пусть в ячейке размером 4 байта хранится следующая последовательность нулей и единиц, шестнадцатеричное представление которой такое: С215999A16. Известно, что здесь хранится вещественное число, т.е. в программе записано, например, объявление: float a. Что это за число в 10-й системе счисления?
Для ответа на этот вопрос в обратном порядке выполняем действия, описанные выше.
1) Запишем двоичное представление числа: 11000010000101011001100110011010.
2) Единица в старшем бите (самая “левая”) означает, что всё вещественное число отрицательное.
3) В следующих 8 битах находится характеристика числа, т.е. x=100001002=8416. Из формулы (1) получаем двоичный порядок числа: p=x-7F16=8416-7F16 =516=510.
4) Из последних 23 разрядов получаем m=0.001010110011001100110102.
5) Поэтому искомое число
a=1.00101011001100110011010*2 5 =100101.0110011001100110102@25.(6) 16@37.410.
Перевод дробной части выполняли следующим образом:
0.(6) 16 = 0.6666616 = 6*16 -1 +6*16 -2 +6*16 -3 +6*16 -4 +6*16 -5 @0.410.
Т.к. это отрицательное число, то получаем ответ: — 37.410
5.2. Объявление объединения.(+)
Объявление типа объединения, которые ещё называют смеси, похоже на объявление структурного типа. Только вместо ключевого слова struct используется union. Как и для структурной переменной, возможны три способа объявления переменной типа объединения: раздельное, совместное и анонимное (см. 1.1).
Для изучения объединения сначала рассмотрим следующий код для работы со структурой.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8557 — | 7410 — или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Доброго времени суток уважаемый пользователь. На этой страничке мы поговорим на такие темы, как: Вещественные числа, Вещественные числа в памяти компьютера.
Предположим, в компьютер встроили устройство, которое переводит числа из десятичной системы счисления в двоичную и обратно. Достаточно ли этого для представления чисел в памяти ЭВМ? Оказывается, нет. Мало научиться записывать числа, важно облегчить процесс автоматизированного выполнения арифметических действий над ними.
Вернемся к первым ЭВМ. Основным видом их «деятельности» были вычисления, но объём оперативной памяти и быстродействие процессора были невелики и инженерам приходилось придумывать разнообразные способы хранения и обработки чисел, чтобы даже сложные расчёты выполнялись за разумное время.
Прямой код
Прямой код — способ представления двоичных чисел с фиксированной запятой. Главным образом используется для записи неотрицательных чисел
Прямой код используется в двух вариантах.
В первом (основной) — для записи только неотрицательных чисел:
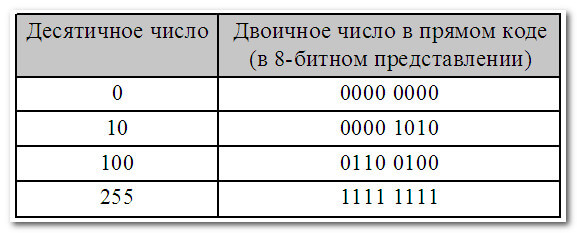
В этом варианте (для восьмибитного двоичного числа) мы можем записать максимальное число 255 (всего чисел 256 — от 0 до 255)
Второй вариант — для записи как положительных, так и отрицательных чисел.
В этом случае старший бит (в нашем случае — восьмой) объявляется знаковым разрядом (знаковым битом).
При этом, если:
— знаковый разряд равен 0, то число положительное
— знаковый разряд равен 1, то число отрицательное

В этом случае диапазон десятичных чисел, которые можно записать в прямом коде составляет от — 127 до +127:
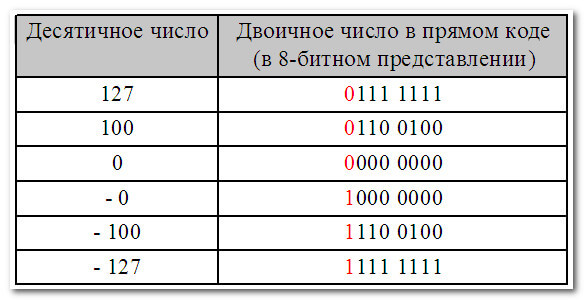
Подводя итоги вопроса, не влезая в его дебри, скажу одно:
Прямой код используется главным образом для представления неотрицательных чисел.
Использование прямого кода для представления отрицательных чисел является неэффективным — очень сложно реализовать арифметические операции и, кроме того, в прямом коде два представления нуля — положительный ноль и отрицательный ноль (чего не бывает):
Немного истории
В 60-е и 70-е годы не было единого стандарта представления чисел с плавающей запятой, способов округления, арифметических операций. В результате программы были крайне не портабельны. Но еще большей проблемой было то, что у разных компьютеров были свои «странности» и их нужно было знать и учитывать в программе. Например, разница двух не равных чисел возвращала ноль. В результате выражения «X=Y» и «X-Y=0» вступали в противоречие. Умельцы обходили эту проблему очень хитрыми трюками, например, делали присваивание «X=(X-X)+X» перед операциями умножения и деления, чтобы избежать проблем.
Инициатива создать единый стандарт для представления чисел с плавающей запятой подозрительно совпала с попытками в 1976 году компанией Intel разработать «лучшую» арифметику для новых сопроцессоров к 8086 и i432. За разработку взялись ученые киты в этой области, проф. Джон Палмер и Уильям Кэхэн. Последний в своем интервью высказал мнение, что серьезность, с которой Intel разрабатывала свою арифметику, заставила другие компании объединиться и начать процесс стандартизации.
Все были настроены серьезно, ведь очень выгодно продвинуть свою архитектуру и сделать ее стандартной. Свои предложения представили компании DEC, National Superconductor, Zilog, Motorola. Производители мейнфреймов Cray и IBM наблюдали со стороны. Компания Intel, разумеется, тоже представила свою новую арифметику. Авторами предложенной спецификации стали Уильям Кэхэн, Джероми Кунен и Гарольд Стоун и их предложение сразу прозвали «K-C-S».
Практически сразу же были отброшены все предложения, кроме двух: VAX от DEC и «K-C-S» от Intel. Спецификация VAX была значительно проще, уже была реализована в компьютерах PDP-11, и было понятно, как на ней получить максимальную производительность. С другой стороны в «K-C-S» содержалось много полезной функциональности, такой как «специальные» и «денормализованные» числа (подробности ниже).
В «K-C-S» все арифметические алгоритмы заданы строго и требуется, чтобы в реализации результат с ними совпадал. Это позволяет выводить строгие выкладки в рамках этой спецификации. Если раньше математик решал задачу численными методами и доказывал свойства решения, не было никакой гарантии, что эти свойства сохранятся в программе. Строгость арифметики «K-C-S» сделала возможным доказательство теорем, опираясь на арифметику с плавающей запятой.
Компания DEC сделала все, чтобы ее спецификацию сделали стандартом. Она даже заручилась поддержкой некоторых авторитетных ученых в том, что арифметика «K-C-S» в принципе не может достигнуть такой же производительности, как у DEC. Ирония в том, что Intel знала, как сделать свою спецификацию такой же производительной, но эти хитрости были коммерческой тайной. Если бы Intel не уступила и не открыла часть секретов, она бы не смогла сдержать натиск DEC.
Подробнее о баталиях при стандартизации смотрите в интервью профессора Кэхэна, а мы рассмотрим, как выглядит представление чисел с плавающей запятой сейчас.
Память
Как вам должно быть уже известно, минимальная единица измерения информации составляет 1 бит. Как мы уже выяснили, представление чисел в компьютере происходит в двоичном формате. Таким образом, каждый бит памяти будет занят одним значением – 1 или 0.
Для хранения больших чисел используются ячейки. Каждая такая единица содержит до 8 бит информации. Поэтому можно сделать вывод, что минимальное значение в каждом отрезке памяти может составлять 1 байт или быть восьмизначным двоичным числом.
Уроки 6 — 7
§ 1.2. Представление чисел в компьютере
Ключевые слова:
Разряд
беззнаковое представление целых чисел
представление целых чисел со знаком
представление вещественных чисел
1.2.1. Представление целых чисел
Оперативная память компьютера состоит из ячеек, каждая из которых представляет собой физическую систему, состоящую из некоторого числа однородных элементов. Эти элементы обладают двумя устойчивыми состояниями, одно из которых соответствует нулю, а другое — единице. Каждый такой элемент служит для хранения одного из битов — разряда двоичного числа. Именно поэтому каждый элемент ячейки называют битом или разрядом (рис. 1.2).
Рис. 1.2. Ячейка памяти
Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (под целые числа обычно отводится 8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда. Беззнаковое представление можно использовать только для неотрицательных целых чисел, отрицательные числа представляются только в знаковом виде.
Беззнаковое представление используется для таких объектов, как адреса ячеек, всевозможные счётчики (например, число символов в тексте), а также числа, обозначающие дату и время, размеры графических изображений в пикселях и т. д.
Максимальное значение целого неотрицательного числа достигается в случае, когда во всех разрядах ячейки хранятся единицы. Для n-разрядного представления оно будет равно 2 n -1. Минимальное число соответствует п нулям, хранящимся в n разрядах памяти, и равно нулю.
Ниже приведены максимальные значения для беззнаковых целых n-разрядных чисел:

Для получения компьютерного представления беззнакового целого числа достаточно перевести число в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
Пример 1 . Число 53 10 = 110101 2 в восьмиразрядном представлении имеет вид:
Это же число 53 в шестнадцати разрядах будет записано следующим образом:
При представлении со знаком самый старший (левый) разряд отводится под знак числа, остальные разряды — под само число. Если число положительное, то в знаковый разряд помещается 0, если число отрицательное — 1. Такое представление чисел называется прямым кодом.
В компьютере прямые коды используются для хранения положительных чисел в запоминающих устройствах, для выполнения операций с положительными числами.
На сайте Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/) размещён информационный модуль «Число и его компьютерный код». С помощью этого ресурса вы можете получить дополнительную информацию по изучаемой теме.
Для выполнения операций с отрицательными числами используется дополнительный код, позволяющий заменить операцию вычитания сложением. Узнать алгоритм образования дополнительного кода вы можете с помощью информационного модуля «Дополнительный код», размещённого на сайте Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/).
1.2.2. Представление вещественных чисел
Любое вещественное число А может быть записано в экспоненциальной форме:

где:
m — мантисса числа;
p — порядок числа.
Например, число 472 ООО ООО может быть представлено так: 4,72 10 8 , 47,2 10 7 , 472,0 10 6 и т. д.
С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида: 4.72Е+8.
Здесь знак «Е» обозначает основание десятичной системы счисления и читается как «умножить на десять в степени».
Из приведённого выше примера видно, что положение запятой в записи числа может изменяться.
Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472 ООО ООО будет представлено как 0,472 10 9 .
Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.
Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.
Максимальное значение порядка числа для приведённого выше примера составляет 1111111 2 = 127 10 , и, следовательно, максимальное значение числа:
0,11111111111111111111111 10 1111111
Попытайтесь самостоятельно выяснить, каков десятичный эквивалент этой величины.
Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.
САМОЕ ГЛАВНОЕ
Для компьютерного представления целых чисел используются несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64) и наличием или отсутствием знакового разряда.
Для представления беззнакового целого числа его следует перевести в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
При представлении со знаком самый старший разряд отводится под знак числа, остальные разряды — под само число. Бели число положительное, то в знаковый разряд помещается 0, если число отрицательное, то 1. Положительные числа хранятся в компьютере в прямом коде, отрицательные — в дополнительном.
При хранении в компьютере вещественных чисел выделяются разряды на хранение знака порядка числа, самого порядка, знака мантиссы и мантиссы. При этом любое число записывается так:

где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.
Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.
2. Как в памяти компьютера представляются целые положительные и отрицательные числа?
3. Любое целое число можно рассматривать как вещественное, но с нулевой дробной частью. Обоснуйте целесообразность наличия особых способов компьютерного представления целых чисел.
4. Представьте число 63 10 в беззнаковом 8-разрядном формате.
5. Найдите десятичные эквиваленты чисел по их прямым кодам, записанным в 8-разрядном формате со знаком:
а) 01001100;
б) 00010101.
6. Какие из чисел 443 8 , 101010 2 , 256 10 можно сохранить в 8-разрядном формате?
7. Запишите следующие числа в естественной форме:
а) 0,3800456 10 2 ;
б) 0,245 10 -3 ;
в) 1,256900Е+5;
г) 9,569120Е-3.
8. Запишите число 2010,0102 10 пятью различными способами в экспоненциальной форме.
9. Запишите следующие числа в экспоненциальной форме с нормализованной мантиссой — правильной дробью, имеющей после запятой цифру, отличную от нуля:
а) 217,934 10 ;
б) 75321 10 ;
в) 0,00101 10 .
10. Изобразите схему, связывающую основные понятия, рассмотренные в данном параграфе.
Тема: Представление чисел в компьютере. Формат с фиксированной и плавающей запятой. Прямой, обратный и дополнительный код.
Повторение: Перевод целых чисел в двоичную систему счисления:
13 10 = а 2 Аналогично:
1345 10 =10101000001 2
Представление целых чисел в компьютере.
Вся информация, обрабатываемая компьютерами, хранится в них в двоичном виде. Каким же образом осуществляется это хранение?
Информация, вводимая в компьютер и возникающая в ходе его работы, хранится в его памяти. Память компьютера можно представить как длинную страницу, состоящую из отдельных строк. Каждая такая строка называется ячейкой памяти .
Ячейка – это часть памяти компьютера, вмещающая в себя информацию, доступную для обработки отдельной командой процессора. Минимальной адресуемой ячейкой памяти называется байт – 8 двоичных разрядов. Порядковый номер байта называется его адресом .
ячейка (8бит = 1байт)
машинным словом.
Ячейка памяти состоит из некоторого числа однородных элементов. Каждый элемент способен находиться в одном из двух состояний и служит для изображения одного из разрядов числа. Именно поэтому каждый элемент ячейки называют разрядом . Нумерацию разрядов в ячейке принято вести справа налево, самый правый разряд имеет порядковый номер 0. Это младший разряд ячейки памяти, старший разряд имеет порядковый номер (n-1) в n-разрядной ячейке памяти.
Содержимым любого разряда может быть либо 0, либо 1.
Содержимое ячейки памяти называется машинным словом. Ячейка памяти разделяется на разряды, в каждом из которых хранится разряд числа.
Например, самые современные персональные компьютеры являются 64-разрядным, то есть машинное слово и соответственно, ячейка памяти, состоит из 64 разрядов или битов .
Бит — минимальная единица измерения информации. Каждый бит может принимать значение 0 или 1. Битом также называют разряд ячейки памяти ЭВМ.
Стандартный размер наименьшей ячейки памяти равен восьми битам, то есть восьми двоичным разрядам. Совокупность из 8 битов является основной единицей представления данных – байт.
Байт (от английского byte – слог) – часть машинного слова, состоящая из 8 бит, обрабатываемая в ЭВМ как одно целое. На экране – ячейка памяти, состоящая из 8 разрядов – это байт. Младший разряд имеет порядковый номер 0, старший разряд – порядковый номер 7.
8 бит = 1 байт
Для представления чисел в памяти компьютера используются два формата: формат с фиксированной точкой и формат с плавающей точкой . В формате с фиксированной точкой представляются только целые числа , в формате с плавающей точкой – вещественные числа (дробные).
В подавляющем большинстве задач, решаемых с помощью ЭВМ, многие действия сводятся к операциям над целыми числами. Сюда относятся задачи экономического характера, при решении которых данными служат количества акций, сотрудников, деталей, транспортных средств и т.д. Целые числа используются для обозначения даты и времени, и для нумерации различных объектов: элементов массивов, записей в базах данных, машинных адресов и т.д.
Целые числа могут представляться в компьютере со знаком или без знака (быть положительными или отрицательными).
Целые числа без знака обычно занимают в памяти один или два байта и принимают в однобайтовом формате значения от 00000000 2 до 11111111 2 , а в двухбайтовом формате — от 00000000 00000000 2 до 11111111 11111111 2 .
Целые числа со знаком обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак «плюс» кодируется нулем, а «минус» — единицей.
1101 2 10101000001 2
Разряд, отводимый под знак
Недостающие до целого байта старшие разряды заполняются нулями.
В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код , обратный код , дополнительный код .
Прямой код – это представление числа в двоичной системе счисления, при этом первый разряд отводится под знак числа. Если число положительное, то в первом разряде находится 0, если число отрицательное, в первом разряде указывается единица.
На самом деле прямой код используется почти исключительно для положительных чисел. Для записи прямого кода числа необходимо:
Представить число в двоичной системе
Дополнить запись числа нулями до предпоследнего старшего разряда 8-ми разрядной или 16-ти разрядной ячейки
Заполнить старший разряд нулем или единицей в зависимости от знака числа.
Пример: число 3 10 в прямом коде однобайтного формата будет представлено в виде:
ч исло -3 10 в прямом коде однобайтного формата имеет вид:
Обратный код для положительного числа в двоичной системе счисления совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1) инвертировать , а в знаковый разряд заносится единица.
Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами вычислительной техникой.
Дополнительный код используют в основном для представления в компьютере отрицательных чисел. Такой код делает арифметические операции более удобными для выполнения их вычислительной техникой.
В дополнительном коде, также как и прямом, первый разряд отводится для представления знака числа. Прямой и дополнительный код для положительных чисел совпадает. Поскольку прямой код используется почти исключительно для представления положительных чисел, а дополнительный – для отрицательных, то почти всегда, если в первом разряде 1, то мы имеем дело с дополнительным кодом. (Ноль обозначает положительное число, а единица – отрицательное).
Алгоритм получения дополнительного кода для отрицательного числа:
1. Найти прямой код числа (перевести число в двоичную систему счисления число без знака)
2. Получить обратный код. Поменять каждый ноль на единицу, а единицу на ноль (инвертировать число)
3. К обратному коду прибавить 1
Пример: Найдем дополнительный код десятичного числа – 47 в 16-ти разрядном формате.
Найдем двоичную запись числа 47 (прямой код).
2. Инвертируем это число (обратный код). 3. Прибавим 1 к обратному коду и получим запись этого числа в оперативной памяти.












